13.4 n queens problem¶
Question
According to the rules of chess, a queen can attack pieces in the same row, column, or on a diagonal line. Given \(n\) queens and an \(n \times n\) chessboard, find arrangements where no two queens can attack each other.
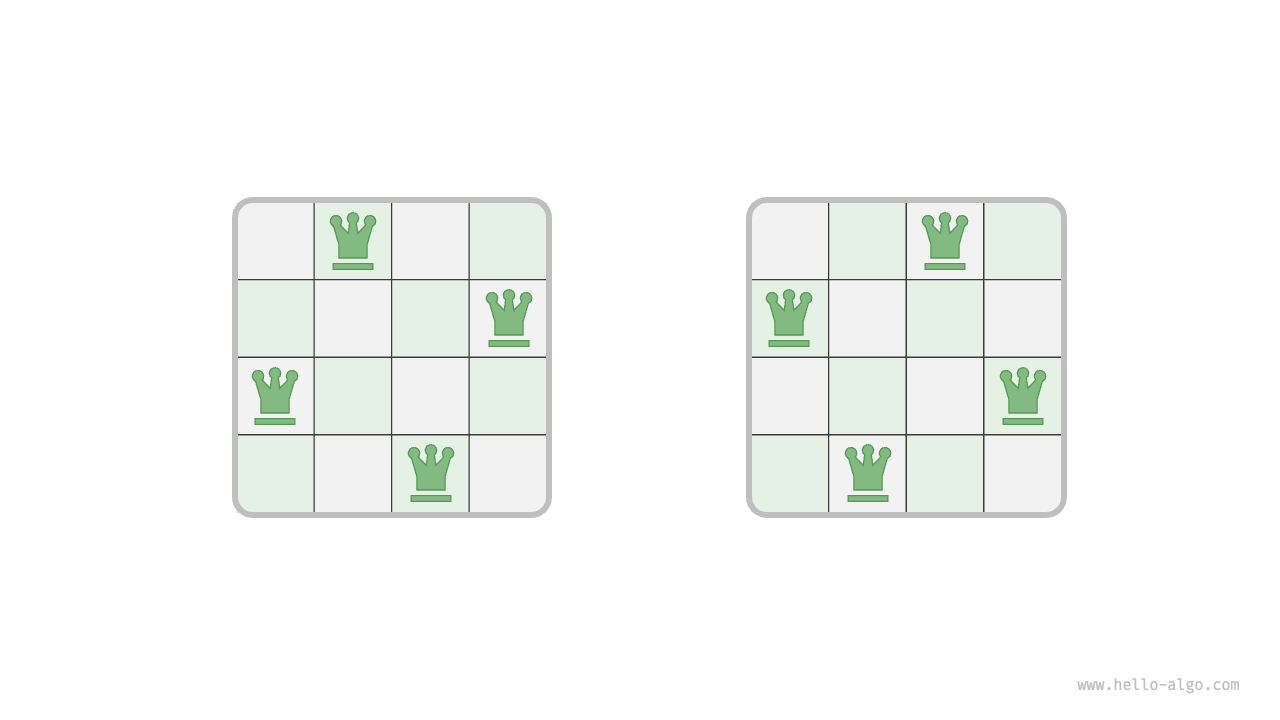
As shown in Figure 13-15, when \(n = 4\), there are two solutions. From the perspective of the backtracking algorithm, an \(n \times n\) chessboard has \(n^2\) squares, presenting all possible choices choices. The state of the chessboard state changes continuously as each queen is placed.
Figure 13-15 Solution to the 4 queens problem
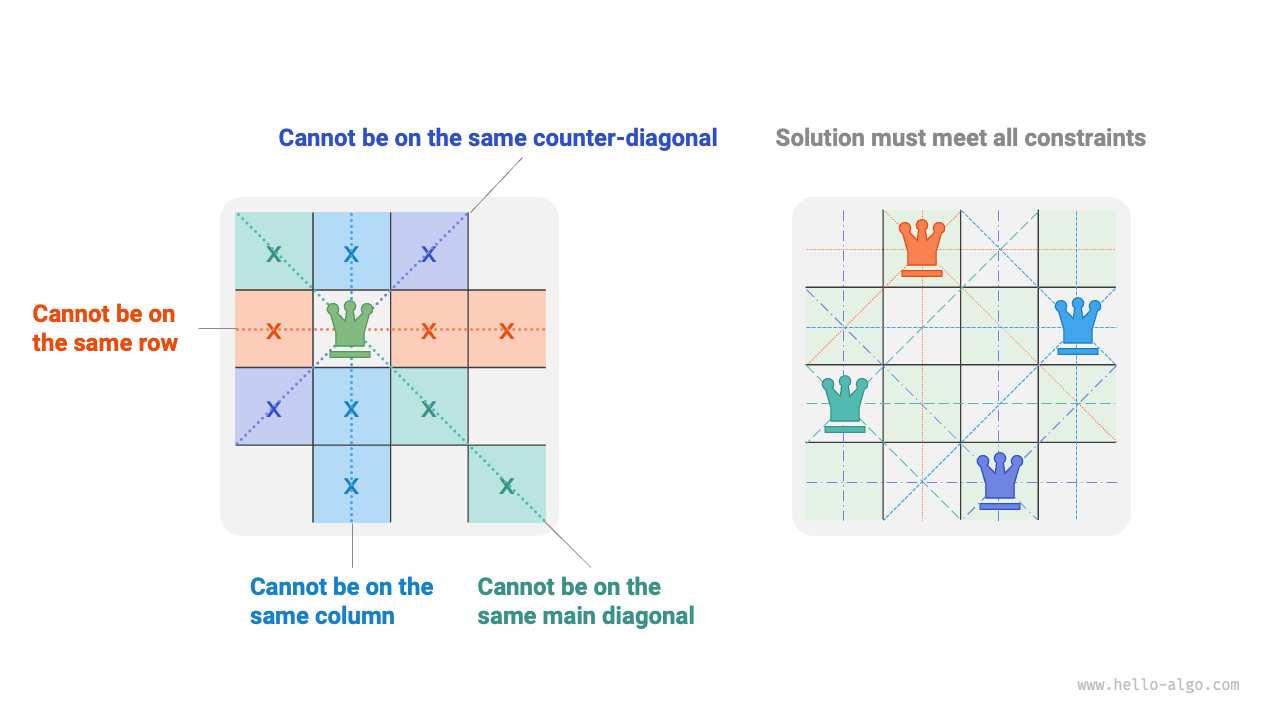
Figure 13-16 shows the three constraints of this problem: multiple queens cannot be on the same row, column, or diagonal. It is important to note that diagonals are divided into the main diagonal \ and the secondary diagonal /.
Figure 13-16 Constraints of the n queens problem
1. Row-by-row placing strategy¶
As the number of queens equals the number of rows on the chessboard, both being \(n\), it is easy to conclude: each row on the chessboard allows and only allows one queen to be placed.
This means that we can adopt a row-by-row placing strategy: starting from the first row, place one queen per row until the last row is reached.
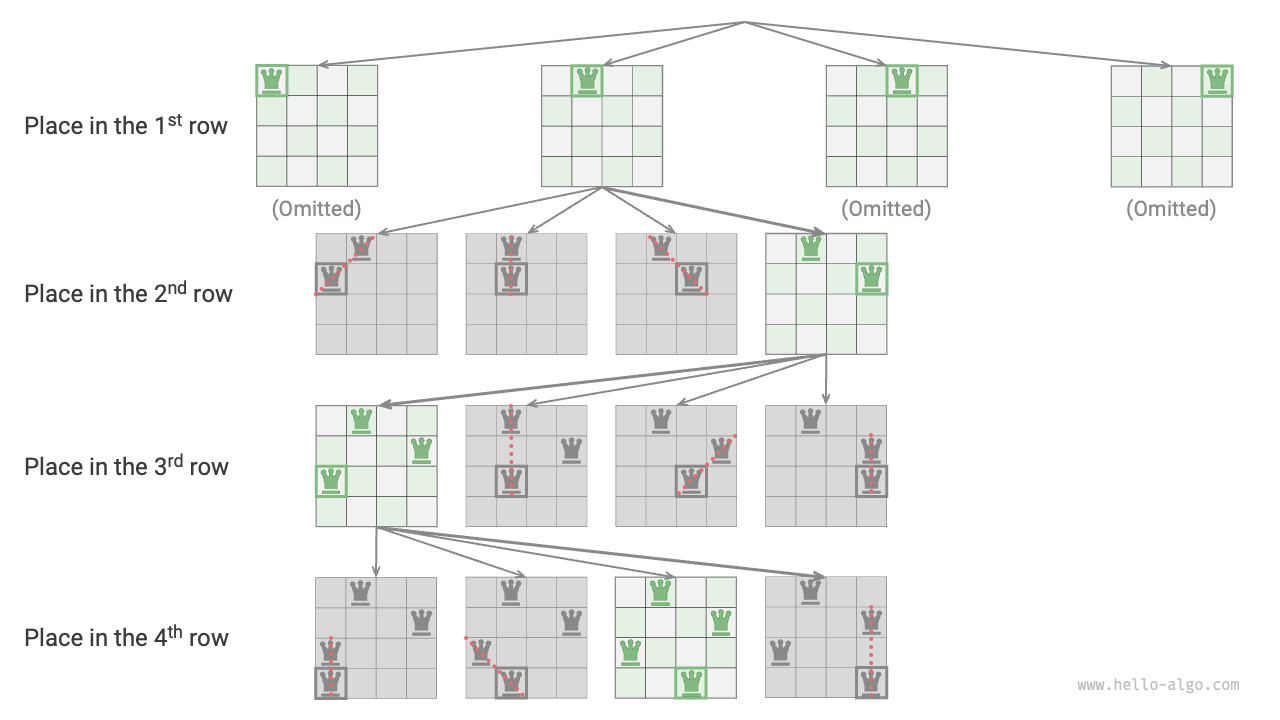
Figure 13-17 shows the row-by-row placing process for the 4 queens problem. Due to space limitations, the figure only expands one search branch of the first row, and prunes any placements that do not meet the column and diagonal constraints.
Figure 13-17 Row-by-row placing strategy
Essentially, the row-by-row placing strategy serves as a pruning function, avoiding all search branches that would place multiple queens in the same row.
2. Column and diagonal pruning¶
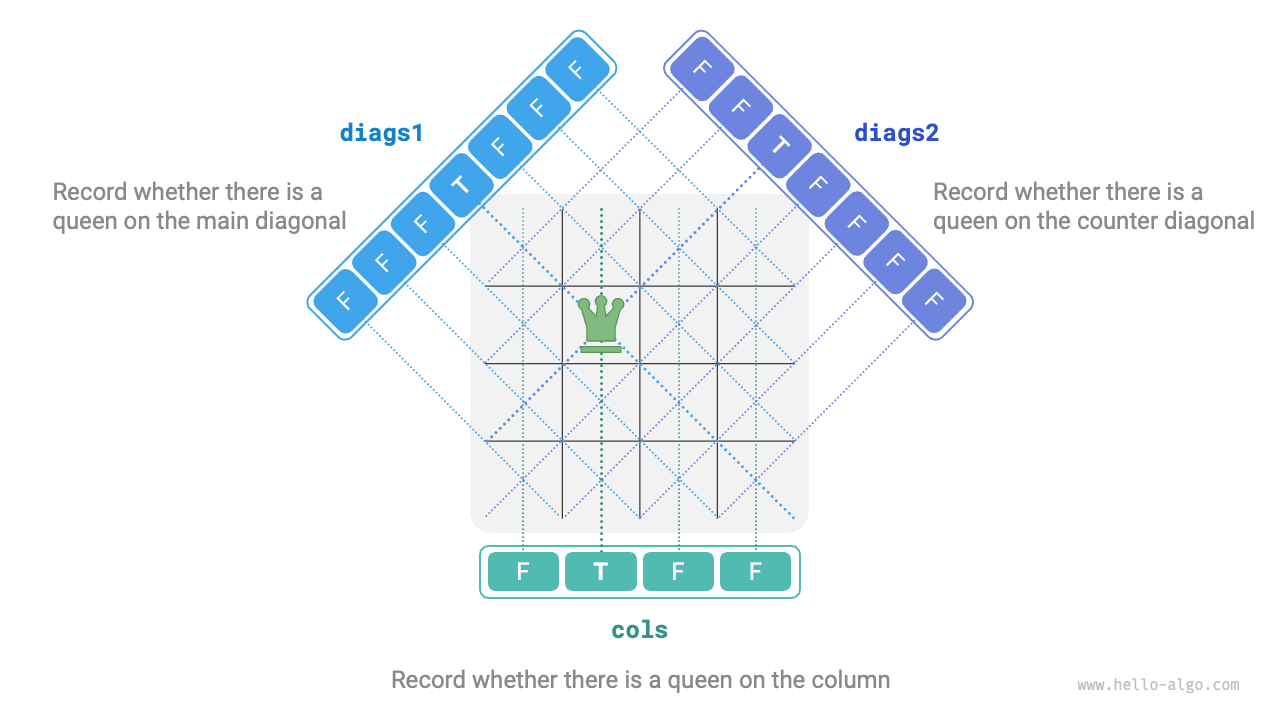
To satisfy column constraints, we can use a boolean array cols of length \(n\) to track whether a queen occupies each column. Before each placement decision, cols is used to prune the columns that already have queens, and it is dynamically updated during backtracking.
How about the diagonal constraints? Let the row and column indices of a cell on the chessboard be \((row, col)\). By selecting a specific main diagonal, we notice that the difference \(row - col\) is the same for all cells on that diagonal, meaning that \(row - col\) is a constant value on that diagonal.
Thus, if two cells satisfy \(row_1 - col_1 = row_2 - col_2\), they are definitely on the same main diagonal. Using this pattern, we can utilize the array diags1 shown in Figure 13-18 to track whether a queen is on any main diagonal.
Similarly, the sum \(row + col\) is a constant value for all cells on a secondary diagonal. We can also use the array diags2 to handle secondary diagonal constraints.
Figure 13-18 Handling column and diagonal constraints
3. Code implementation¶
Please note, in an \(n\)-dimensional matrix, the range of \(row - col\) is \([-n + 1, n - 1]\), and the range of \(row + col\) is \([0, 2n - 2]\), thus the number of both main and secondary diagonals is \(2n - 1\), meaning the length of both arrays diags1 and diags2 is \(2n - 1\).
def backtrack(
row: int,
n: int,
state: list[list[str]],
res: list[list[list[str]]],
cols: list[bool],
diags1: list[bool],
diags2: list[bool],
):
"""Backtracking algorithm: n queens"""
# When all rows are placed, record the solution
if row == n:
res.append([list(row) for row in state])
return
# Traverse all columns
for col in range(n):
# Calculate the main and minor diagonals corresponding to the cell
diag1 = row - col + n - 1
diag2 = row + col
# Pruning: do not allow queens on the column, main diagonal, or minor diagonal of the cell
if not cols[col] and not diags1[diag1] and not diags2[diag2]:
# Attempt: place the queen in the cell
state[row][col] = "Q"
cols[col] = diags1[diag1] = diags2[diag2] = True
# Place the next row
backtrack(row + 1, n, state, res, cols, diags1, diags2)
# Retract: restore the cell to an empty spot
state[row][col] = "#"
cols[col] = diags1[diag1] = diags2[diag2] = False
def n_queens(n: int) -> list[list[list[str]]]:
"""Solve n queens"""
# Initialize an n*n size chessboard, where 'Q' represents the queen and '#' represents an empty spot
state = [["#" for _ in range(n)] for _ in range(n)]
cols = [False] * n # Record columns with queens
diags1 = [False] * (2 * n - 1) # Record main diagonals with queens
diags2 = [False] * (2 * n - 1) # Record minor diagonals with queens
res = []
backtrack(0, n, state, res, cols, diags1, diags2)
return res
/* Backtracking algorithm: n queens */
void backtrack(int row, int n, vector<vector<string>> &state, vector<vector<vector<string>>> &res, vector<bool> &cols,
vector<bool> &diags1, vector<bool> &diags2) {
// When all rows are placed, record the solution
if (row == n) {
res.push_back(state);
return;
}
// Traverse all columns
for (int col = 0; col < n; col++) {
// Calculate the main and minor diagonals corresponding to the cell
int diag1 = row - col + n - 1;
int diag2 = row + col;
// Pruning: do not allow queens on the column, main diagonal, or minor diagonal of the cell
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// Attempt: place the queen in the cell
state[row][col] = "Q";
cols[col] = diags1[diag1] = diags2[diag2] = true;
// Place the next row
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// Retract: restore the cell to an empty spot
state[row][col] = "#";
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* Solve n queens */
vector<vector<vector<string>>> nQueens(int n) {
// Initialize an n*n size chessboard, where 'Q' represents the queen and '#' represents an empty spot
vector<vector<string>> state(n, vector<string>(n, "#"));
vector<bool> cols(n, false); // Record columns with queens
vector<bool> diags1(2 * n - 1, false); // Record main diagonals with queens
vector<bool> diags2(2 * n - 1, false); // Record minor diagonals with queens
vector<vector<vector<string>>> res;
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* Backtracking algorithm: n queens */
void backtrack(int row, int n, List<List<String>> state, List<List<List<String>>> res,
boolean[] cols, boolean[] diags1, boolean[] diags2) {
// When all rows are placed, record the solution
if (row == n) {
List<List<String>> copyState = new ArrayList<>();
for (List<String> sRow : state) {
copyState.add(new ArrayList<>(sRow));
}
res.add(copyState);
return;
}
// Traverse all columns
for (int col = 0; col < n; col++) {
// Calculate the main and minor diagonals corresponding to the cell
int diag1 = row - col + n - 1;
int diag2 = row + col;
// Pruning: do not allow queens on the column, main diagonal, or minor diagonal of the cell
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// Attempt: place the queen in the cell
state.get(row).set(col, "Q");
cols[col] = diags1[diag1] = diags2[diag2] = true;
// Place the next row
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// Retract: restore the cell to an empty spot
state.get(row).set(col, "#");
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* Solve n queens */
List<List<List<String>>> nQueens(int n) {
// Initialize an n*n size chessboard, where 'Q' represents the queen and '#' represents an empty spot
List<List<String>> state = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<String> row = new ArrayList<>();
for (int j = 0; j < n; j++) {
row.add("#");
}
state.add(row);
}
boolean[] cols = new boolean[n]; // Record columns with queens
boolean[] diags1 = new boolean[2 * n - 1]; // Record main diagonals with queens
boolean[] diags2 = new boolean[2 * n - 1]; // Record minor diagonals with queens
List<List<List<String>>> res = new ArrayList<>();
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
Placing \(n\) queens row-by-row, considering column constraints, from the first row to the last row there are \(n\), \(n-1\), \(\dots\), \(2\), \(1\) choices, using \(O(n!)\) time. When recording a solution, it is necessary to copy the matrix state and add it to res, with the copying operation using \(O(n^2)\) time. Therefore, the overall time complexity is \(O(n! \cdot n^2)\). In practice, pruning based on diagonal constraints can significantly reduce the search space, thus often the search efficiency is better than the above time complexity.
Array state uses \(O(n^2)\) space, and arrays cols, diags1, and diags2 each use \(O(n)\) space. The maximum recursion depth is \(n\), using \(O(n)\) stack space. Therefore, the space complexity is \(O(n^2)\).