15.4 Maximum product cutting problem¶
Question
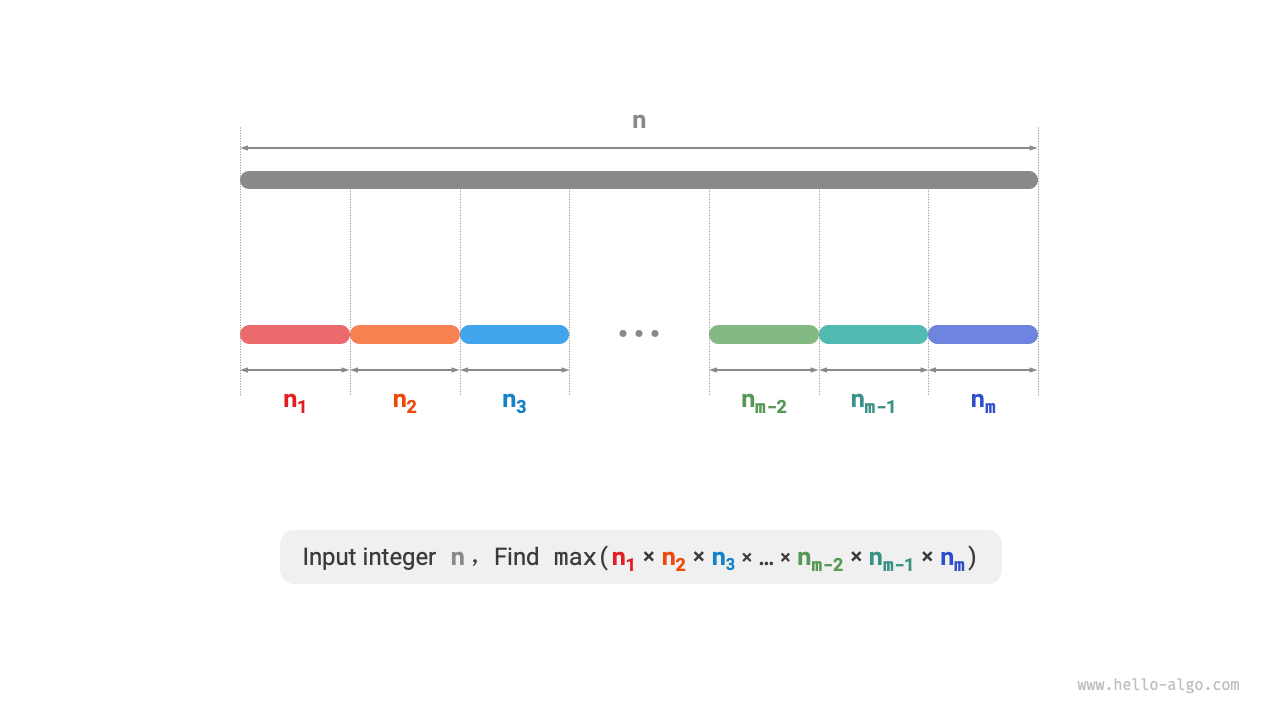
Given a positive integer \(n\), split it into at least two positive integers that sum up to \(n\), and find the maximum product of these integers, as illustrated in Figure 15-13.
Figure 15-13 Definition of the maximum product cutting problem
Assume we split \(n\) into \(m\) integer factors, where the \(i\)-th factor is denoted as \(n_i\), that is,
The goal of this problem is to find the maximum product of all integer factors, namely,
We need to consider: How large should the number of splits \(m\) be, and what should each \(n_i\) be?
1. Greedy strategy determination¶
Experience suggests that the product of two integers is often greater than their sum. Suppose we split a factor of \(2\) from \(n\), then their product is \(2(n-2)\). Compare this product with \(n\):
As shown in Figure 15-14, when \(n \geq 4\), splitting out a \(2\) increases the product, which indicates that integers greater than or equal to \(4\) should be split.
Greedy strategy one: If the splitting scheme includes factors \(\geq 4\), they should be further split. The final split should only include factors \(1\), \(2\), and \(3\).
Figure 15-14 Product increase due to splitting
Next, consider which factor is optimal. Among the factors \(1\), \(2\), and \(3\), clearly \(1\) is the worst, as \(1 \times (n-1) < n\) always holds, meaning splitting out \(1\) actually decreases the product.
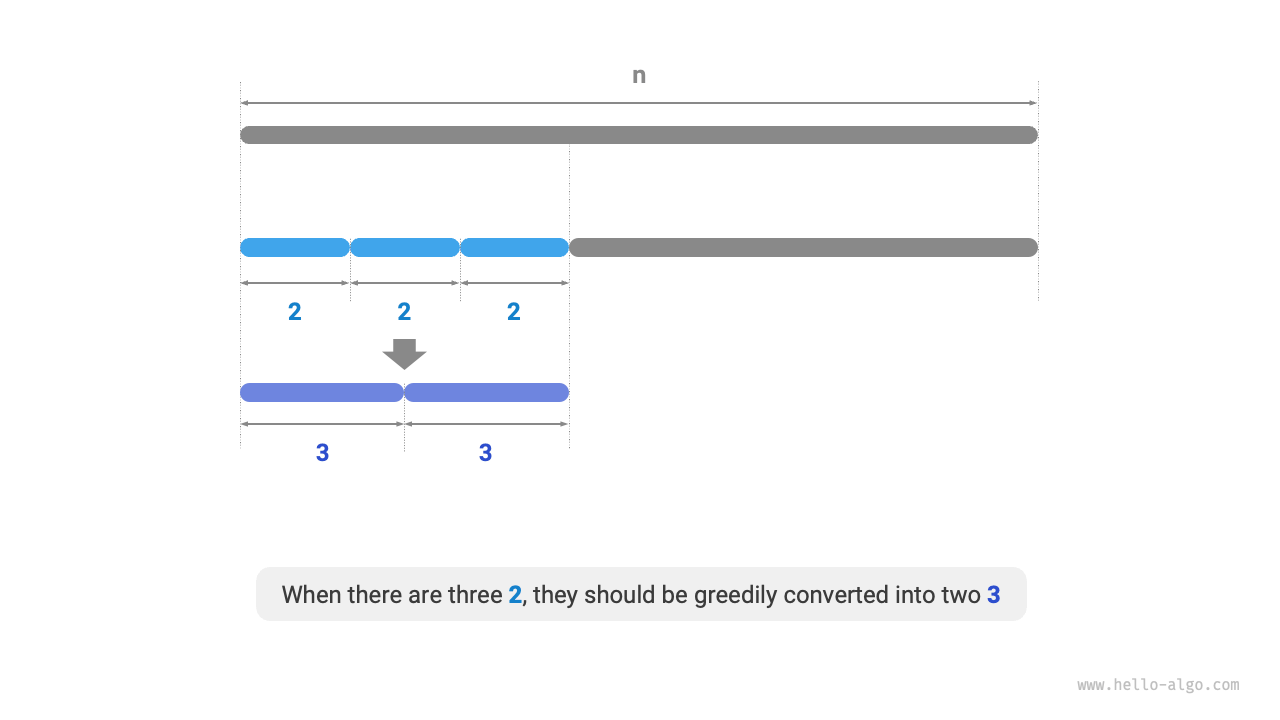
As shown in Figure 15-15, when \(n = 6\), \(3 \times 3 > 2 \times 2 \times 2\). This means splitting out \(3\) is better than splitting out \(2\).
Greedy strategy two: In the splitting scheme, there should be at most two \(2\)s. Because three \(2\)s can always be replaced by two \(3\)s to obtain a higher product.
Figure 15-15 Optimal splitting factors
From the above, the following greedy strategies can be derived.
- Input integer \(n\), continually split out factor \(3\) until the remainder is \(0\), \(1\), or \(2\).
- When the remainder is \(0\), it means \(n\) is a multiple of \(3\), so no further action is taken.
- When the remainder is \(2\), do not continue to split, keep it.
- When the remainder is \(1\), since \(2 \times 2 > 1 \times 3\), the last \(3\) should be replaced with \(2\).
2. Code implementation¶
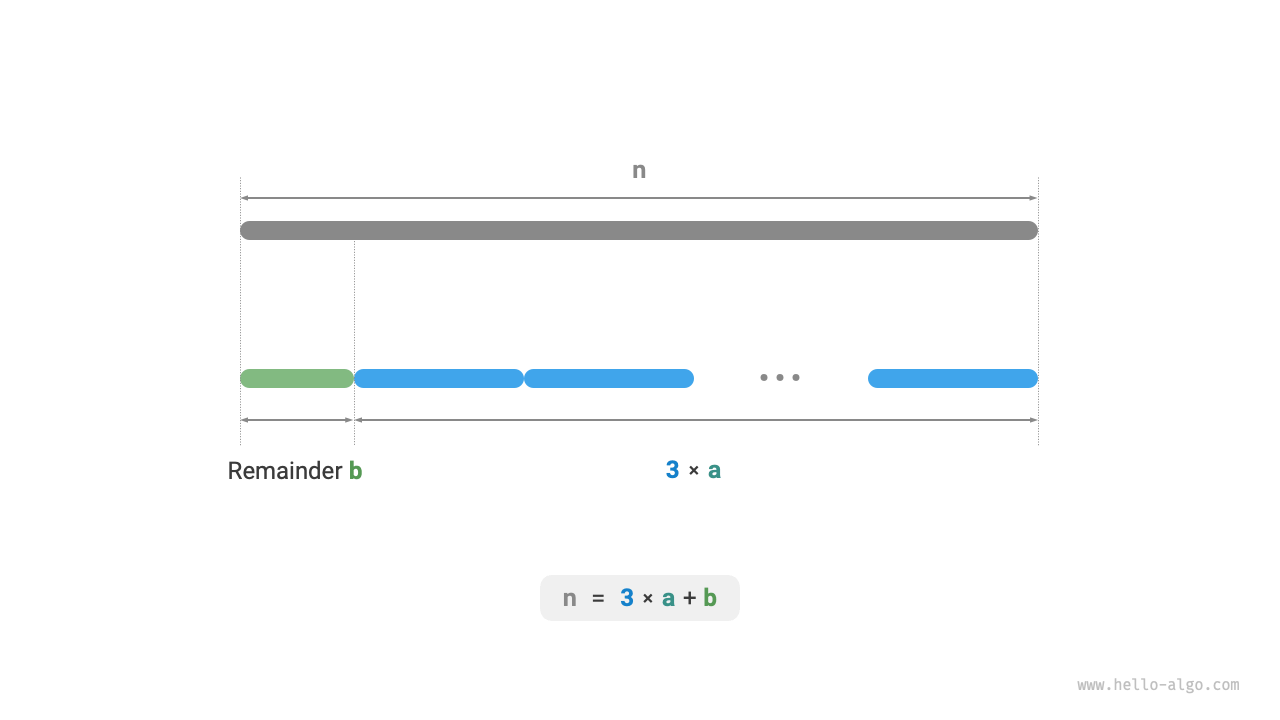
As shown in Figure 15-16, we do not need to use loops to split the integer but can use the floor division operation to get the number of \(3\)s, \(a\), and the modulo operation to get the remainder, \(b\), thus:
Please note, for the boundary case where \(n \leq 3\), a \(1\) must be split out, with a product of \(1 \times (n - 1)\).
def max_product_cutting(n: int) -> int:
"""Maximum product of cutting: Greedy"""
# When n <= 3, must cut out a 1
if n <= 3:
return 1 * (n - 1)
# Greedy cut out 3s, a is the number of 3s, b is the remainder
a, b = n // 3, n % 3
if b == 1:
# When the remainder is 1, convert a pair of 1 * 3 into 2 * 2
return int(math.pow(3, a - 1)) * 2 * 2
if b == 2:
# When the remainder is 2, do nothing
return int(math.pow(3, a)) * 2
# When the remainder is 0, do nothing
return int(math.pow(3, a))
/* Maximum product of cutting: Greedy */
int maxProductCutting(int n) {
// When n <= 3, must cut out a 1
if (n <= 3) {
return 1 * (n - 1);
}
// Greedy cut out 3s, a is the number of 3s, b is the remainder
int a = n / 3;
int b = n % 3;
if (b == 1) {
// When the remainder is 1, convert a pair of 1 * 3 into 2 * 2
return (int)pow(3, a - 1) * 2 * 2;
}
if (b == 2) {
// When the remainder is 2, do nothing
return (int)pow(3, a) * 2;
}
// When the remainder is 0, do nothing
return (int)pow(3, a);
}
/* Maximum product of cutting: Greedy */
int maxProductCutting(int n) {
// When n <= 3, must cut out a 1
if (n <= 3) {
return 1 * (n - 1);
}
// Greedy cut out 3s, a is the number of 3s, b is the remainder
int a = n / 3;
int b = n % 3;
if (b == 1) {
// When the remainder is 1, convert a pair of 1 * 3 into 2 * 2
return (int) Math.pow(3, a - 1) * 2 * 2;
}
if (b == 2) {
// When the remainder is 2, do nothing
return (int) Math.pow(3, a) * 2;
}
// When the remainder is 0, do nothing
return (int) Math.pow(3, a);
}
Figure 15-16 Calculation method of the maximum product after cutting
Time complexity depends on the implementation of the power operation in the programming language. For Python, the commonly used power calculation functions are three types:
- Both the operator
**and the functionpow()have a time complexity of \(O(\log a)\). - The
math.pow()function internally calls the C language library'spow()function, performing floating-point exponentiation, with a time complexity of \(O(1)\).
Variables \(a\) and \(b\) use constant size of extra space, hence the space complexity is \(O(1)\).
3. Correctness proof¶
Using the proof by contradiction, only analyze cases where \(n \geq 3\).
- All factors \(\leq 3\): Assume the optimal splitting scheme includes a factor \(x \geq 4\), then it can definitely be further split into \(2(x-2)\), obtaining a larger product. This contradicts the assumption.
- The splitting scheme does not contain \(1\): Assume the optimal splitting scheme includes a factor of \(1\), then it can definitely be merged into another factor to obtain a larger product. This contradicts the assumption.
- The splitting scheme contains at most two \(2\)s: Assume the optimal splitting scheme includes three \(2\)s, then they can definitely be replaced by two \(3\)s, achieving a higher product. This contradicts the assumption.