11.4 Insertion sort¶
Insertion sort is a simple sorting algorithm that works very much like the process of manually sorting a deck of cards.
Specifically, we select a pivot element from the unsorted interval, compare it with the elements in the sorted interval to its left, and insert the element into the correct position.
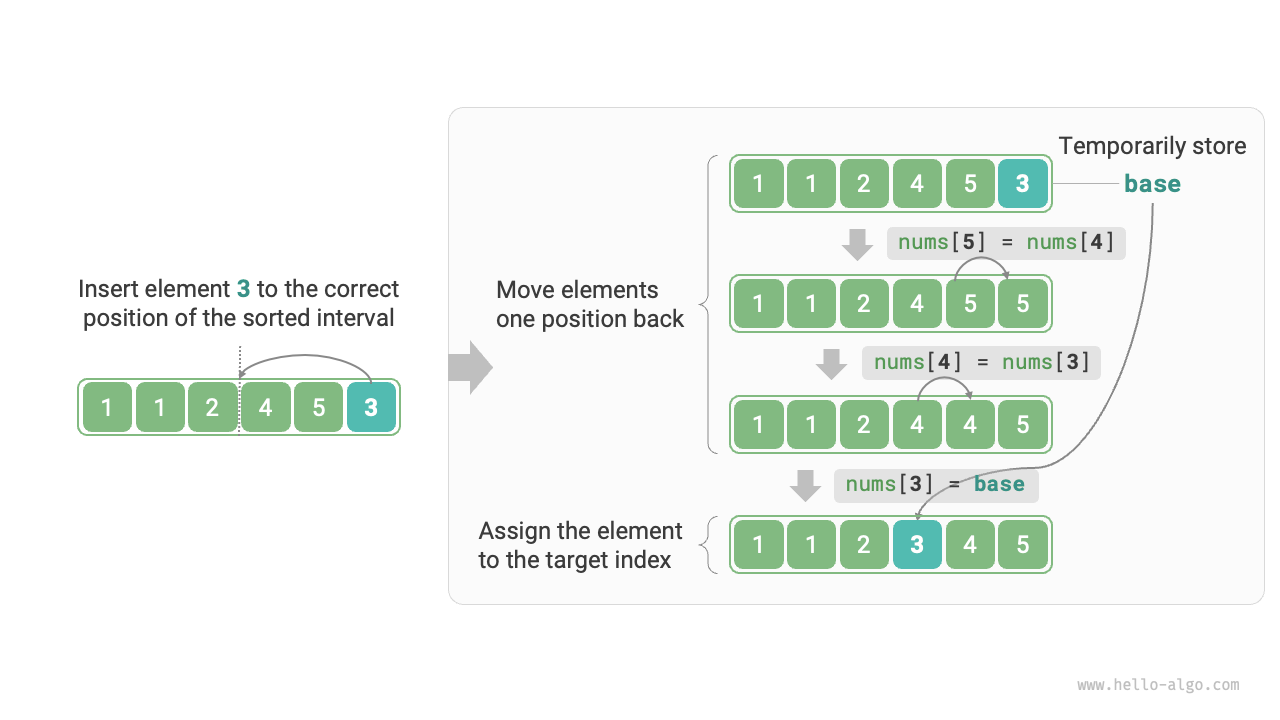
Figure 11-6 shows the process of inserting an element into an array. Assuming the pivot element is base, we need to move all elements between the target index and base one position to the right, then assign base to the target index.
Figure 11-6 Single insertion operation
11.4.1 Algorithm process¶
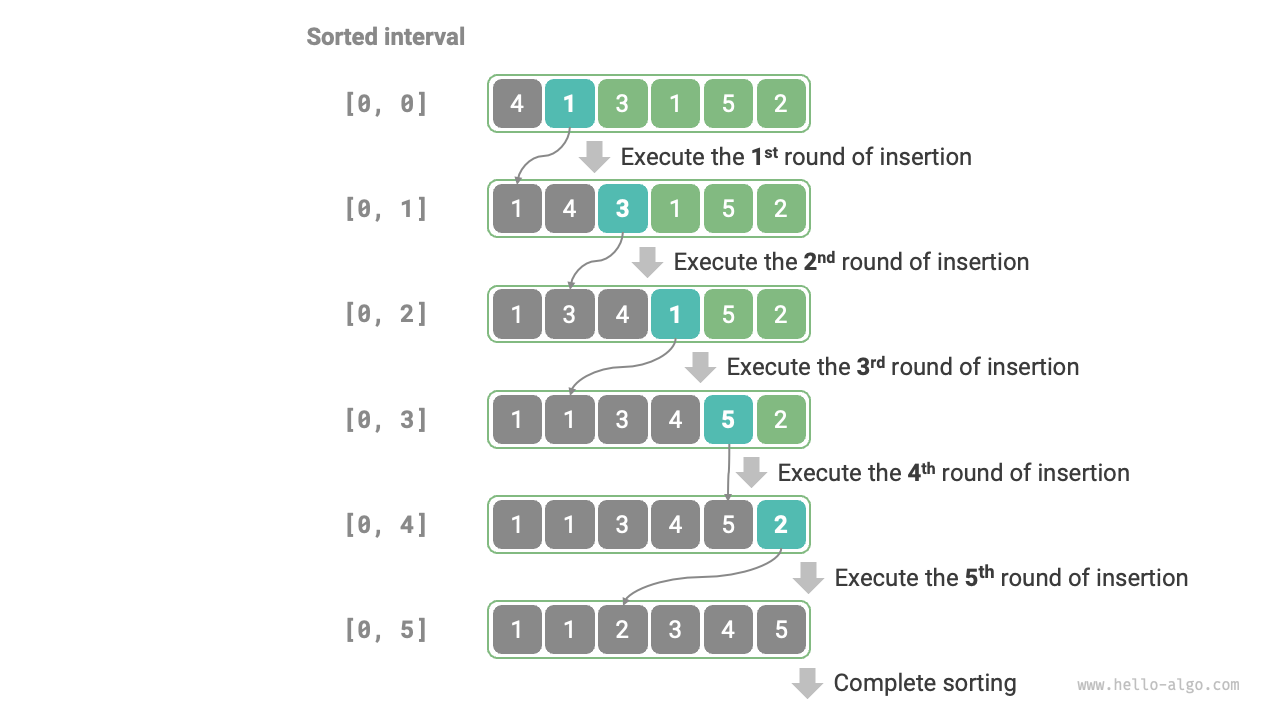
The overall process of insertion sort is shown in Figure 11-7.
- Initially, the first element of the array is sorted.
- The second element of the array is taken as
base, and after inserting it into the correct position, the first two elements of the array are sorted. - The third element is taken as
base, and after inserting it into the correct position, the first three elements of the array are sorted. - And so on, in the last round, the last element is taken as
base, and after inserting it into the correct position, all elements are sorted.
Figure 11-7 Insertion sort process
Example code is as follows:
def insertion_sort(nums: list[int]):
"""Insertion sort"""
# Outer loop: sorted range is [0, i-1]
for i in range(1, len(nums)):
base = nums[i]
j = i - 1
# Inner loop: insert base into the correct position within the sorted range [0, i-1]
while j >= 0 and nums[j] > base:
nums[j + 1] = nums[j] # Move nums[j] to the right by one position
j -= 1
nums[j + 1] = base # Assign base to the correct position
/* Insertion sort */
void insertionSort(vector<int> &nums) {
// Outer loop: sorted range is [0, i-1]
for (int i = 1; i < nums.size(); i++) {
int base = nums[i], j = i - 1;
// Inner loop: insert base into the correct position within the sorted range [0, i-1]
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j]; // Move nums[j] to the right by one position
j--;
}
nums[j + 1] = base; // Assign base to the correct position
}
}
/* Insertion sort */
void insertionSort(int[] nums) {
// Outer loop: sorted range is [0, i-1]
for (int i = 1; i < nums.length; i++) {
int base = nums[i], j = i - 1;
// Inner loop: insert base into the correct position within the sorted range [0, i-1]
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j]; // Move nums[j] to the right by one position
j--;
}
nums[j + 1] = base; // Assign base to the correct position
}
}
11.4.2 Algorithm characteristics¶
- Time complexity is \(O(n^2)\), adaptive sorting: In the worst case, each insertion operation requires \(n - 1\), \(n-2\), ..., \(2\), \(1\) loops, summing up to \((n - 1) n / 2\), thus the time complexity is \(O(n^2)\). In the case of ordered data, the insertion operation will terminate early. When the input array is completely ordered, insertion sort achieves the best time complexity of \(O(n)\).
- Space complexity is \(O(1)\), in-place sorting: Pointers \(i\) and \(j\) use a constant amount of extra space.
- Stable sorting: During the insertion operation, we insert elements to the right of equal elements, not changing their order.
11.4.3 Advantages of insertion sort¶
The time complexity of insertion sort is \(O(n^2)\), while the time complexity of quicksort, which we will study next, is \(O(n \log n)\). Although insertion sort has a higher time complexity, it is usually faster in cases of small data volumes.
This conclusion is similar to that for linear and binary search. Algorithms like quicksort that have a time complexity of \(O(n \log n)\) and are based on the divide-and-conquer strategy often involve more unit operations. In cases of small data volumes, the numerical values of \(n^2\) and \(n \log n\) are close, and complexity does not dominate, with the number of unit operations per round playing a decisive role.
In fact, many programming languages (such as Java) use insertion sort in their built-in sorting functions. The general approach is: for long arrays, use sorting algorithms based on divide-and-conquer strategies, such as quicksort; for short arrays, use insertion sort directly.
Although bubble sort, selection sort, and insertion sort all have a time complexity of \(O(n^2)\), in practice, insertion sort is used significantly more frequently than bubble sort and selection sort, mainly for the following reasons.
- Bubble sort is based on element swapping, which requires the use of a temporary variable, involving 3 unit operations; insertion sort is based on element assignment, requiring only 1 unit operation. Therefore, the computational overhead of bubble sort is generally higher than that of insertion sort.
- The time complexity of selection sort is always \(O(n^2)\). Given a set of partially ordered data, insertion sort is usually more efficient than selection sort.
- Selection sort is unstable and cannot be applied to multi-level sorting.