9.3 Graph traversal¶
Trees represent a "one-to-many" relationship, while graphs have a higher degree of freedom and can represent any "many-to-many" relationship. Therefore, we can consider tree as a special case of graph. Clearly, tree traversal operations are also a special case of graph traversal operations.
Both graphs and trees require the application of search algorithms to implement traversal operations. Graph traversal can be divided into two types: Breadth-First Search (BFS) and Depth-First Search (DFS).
9.3.1 Breadth-first search¶
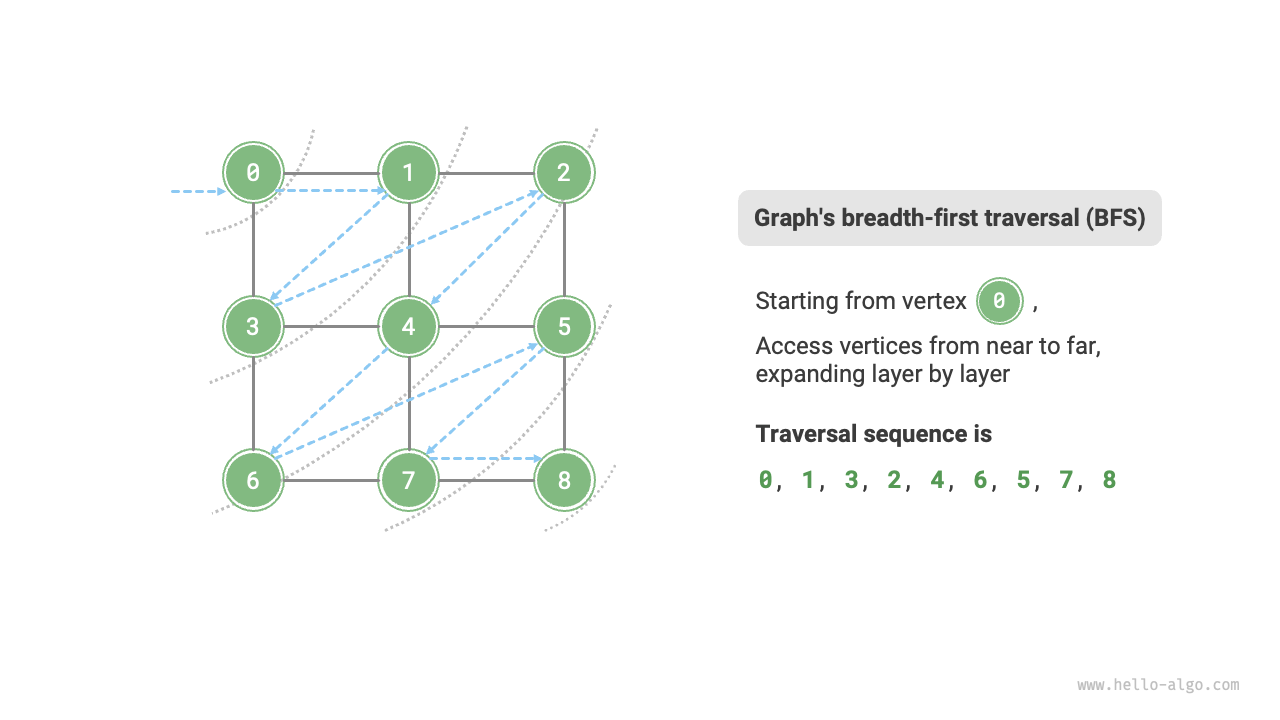
Breadth-first search is a near-to-far traversal method, starting from a certain node, always prioritizing the visit to the nearest vertices and expanding outwards layer by layer. As shown in Figure 9-9, starting from the top left vertex, first traverse all adjacent vertices of that vertex, then traverse all adjacent vertices of the next vertex, and so on, until all vertices have been visited.
Figure 9-9 Breadth-first traversal of a graph
1. Algorithm implementation¶
BFS is usually implemented with the help of a queue, as shown in the code below. The queue is "first in, first out", which aligns with the BFS idea of traversing "from near to far".
- Add the starting vertex
startVetto the queue and start the loop. - In each iteration of the loop, pop the vertex at the front of the queue and record it as visited, then add all adjacent vertices of that vertex to the back of the queue.
- Repeat step
2.until all vertices have been visited.
To prevent revisiting vertices, we use a hash set visited to record which nodes have been visited.
def graph_bfs(graph: GraphAdjList, start_vet: Vertex) -> list[Vertex]:
"""Breadth-first traversal"""
# Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
# Vertex traversal sequence
res = []
# Hash set, used to record visited vertices
visited = set[Vertex]([start_vet])
# Queue used to implement BFS
que = deque[Vertex]([start_vet])
# Starting from vertex vet, loop until all vertices are visited
while len(que) > 0:
vet = que.popleft() # Dequeue the vertex at the head of the queue
res.append(vet) # Record visited vertex
# Traverse all adjacent vertices of that vertex
for adj_vet in graph.adj_list[vet]:
if adj_vet in visited:
continue # Skip already visited vertices
que.append(adj_vet) # Only enqueue unvisited vertices
visited.add(adj_vet) # Mark the vertex as visited
# Return the vertex traversal sequence
return res
/* Breadth-first traversal */
// Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
vector<Vertex *> graphBFS(GraphAdjList &graph, Vertex *startVet) {
// Vertex traversal sequence
vector<Vertex *> res;
// Hash set, used to record visited vertices
unordered_set<Vertex *> visited = {startVet};
// Queue used to implement BFS
queue<Vertex *> que;
que.push(startVet);
// Starting from vertex vet, loop until all vertices are visited
while (!que.empty()) {
Vertex *vet = que.front();
que.pop(); // Dequeue the vertex at the head of the queue
res.push_back(vet); // Record visited vertex
// Traverse all adjacent vertices of that vertex
for (auto adjVet : graph.adjList[vet]) {
if (visited.count(adjVet))
continue; // Skip already visited vertices
que.push(adjVet); // Only enqueue unvisited vertices
visited.emplace(adjVet); // Mark the vertex as visited
}
}
// Return the vertex traversal sequence
return res;
}
/* Breadth-first traversal */
// Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
// Vertex traversal sequence
List<Vertex> res = new ArrayList<>();
// Hash set, used to record visited vertices
Set<Vertex> visited = new HashSet<>();
visited.add(startVet);
// Queue used to implement BFS
Queue<Vertex> que = new LinkedList<>();
que.offer(startVet);
// Starting from vertex vet, loop until all vertices are visited
while (!que.isEmpty()) {
Vertex vet = que.poll(); // Dequeue the vertex at the head of the queue
res.add(vet); // Record visited vertex
// Traverse all adjacent vertices of that vertex
for (Vertex adjVet : graph.adjList.get(vet)) {
if (visited.contains(adjVet))
continue; // Skip already visited vertices
que.offer(adjVet); // Only enqueue unvisited vertices
visited.add(adjVet); // Mark the vertex as visited
}
}
// Return the vertex traversal sequence
return res;
}
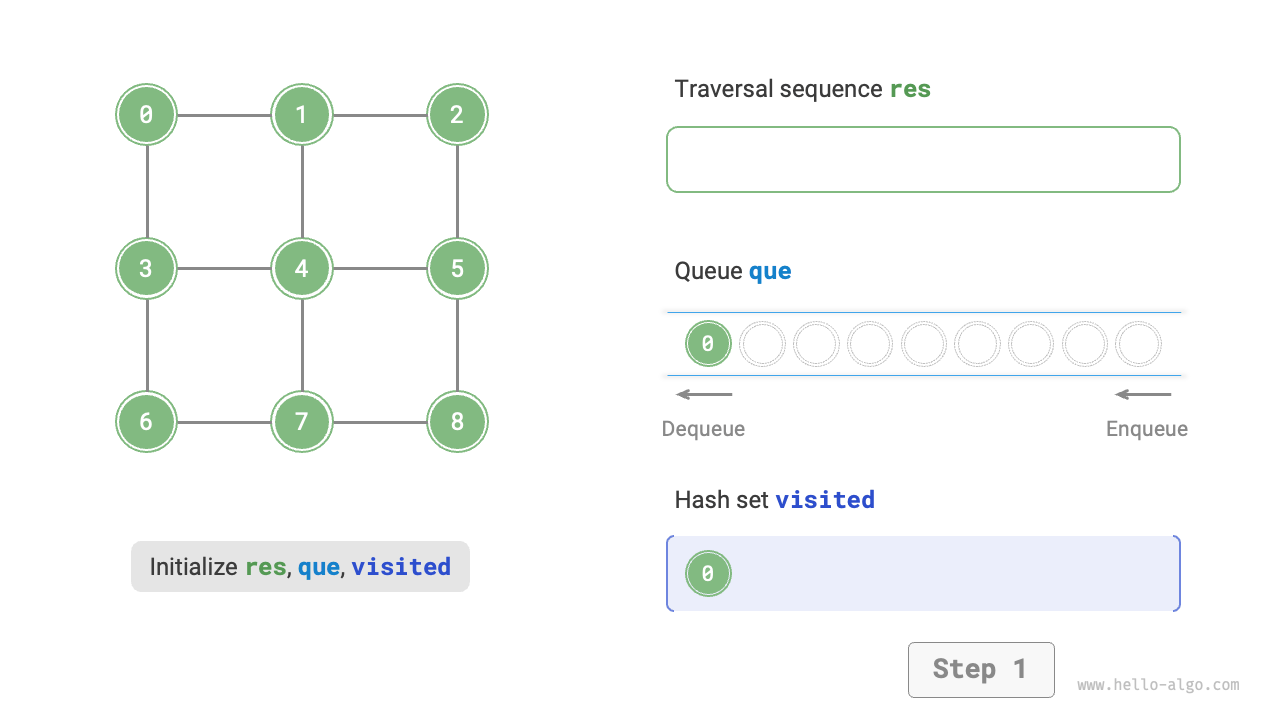
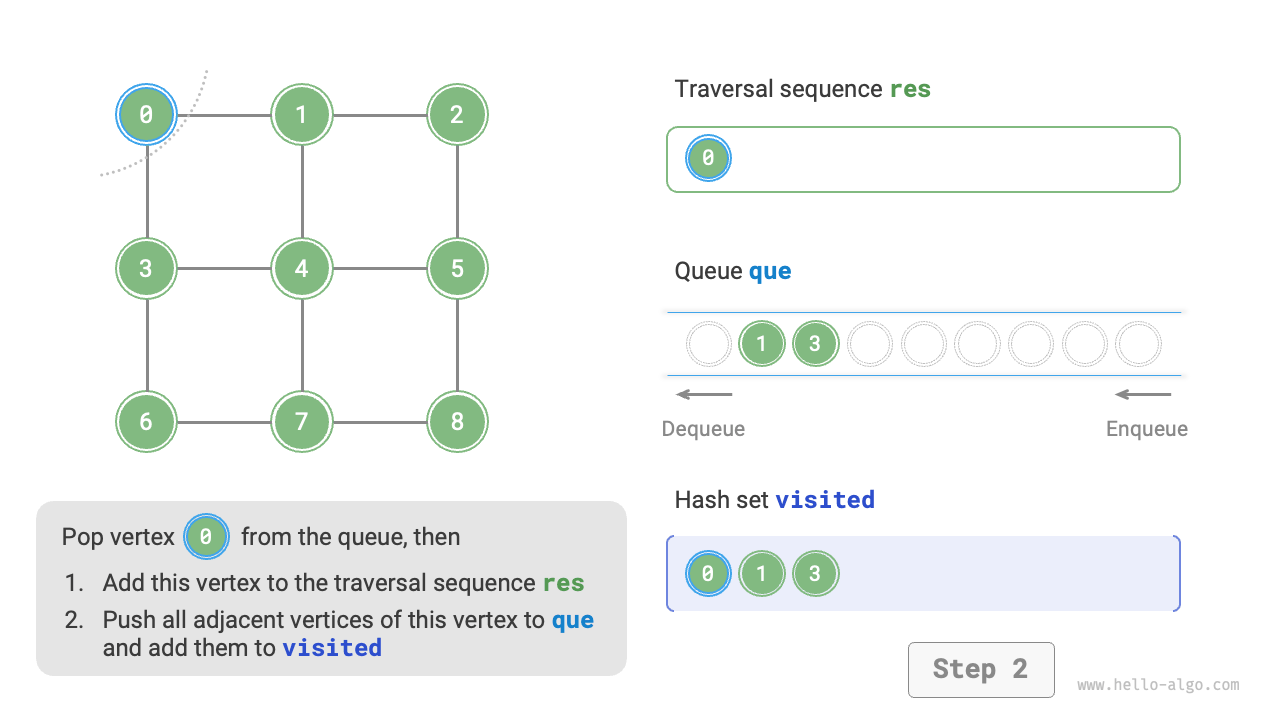
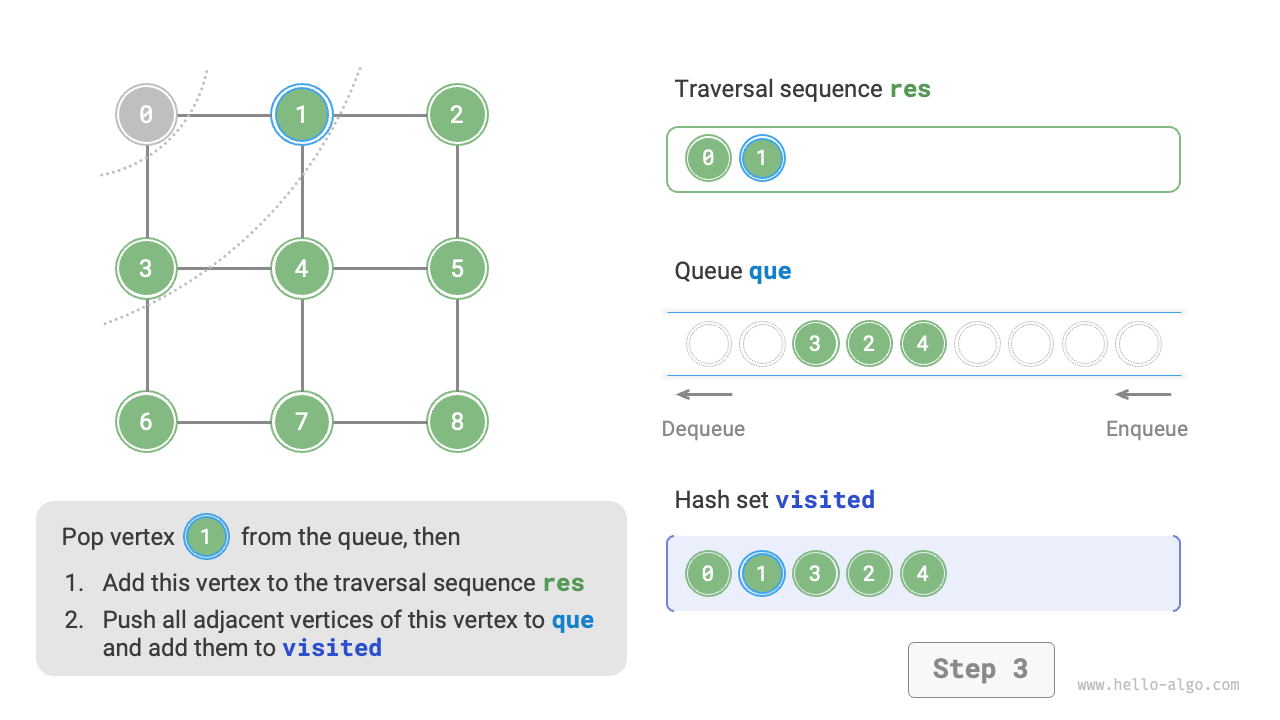
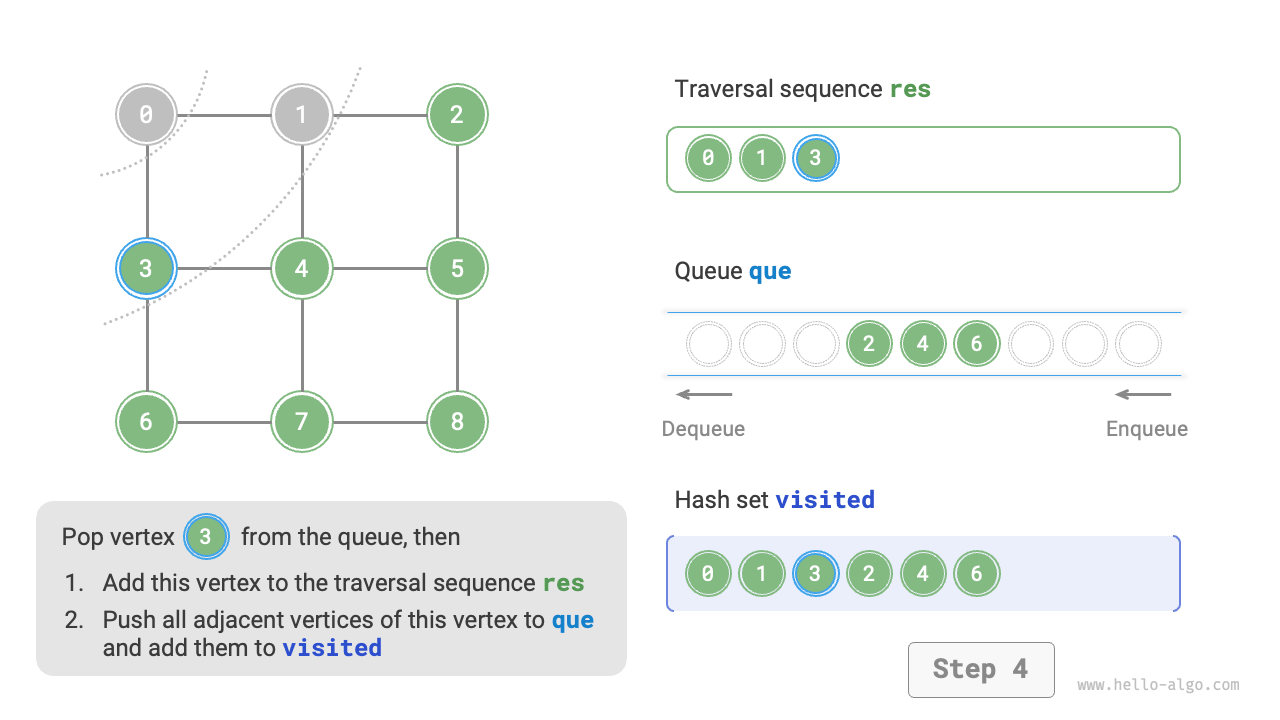
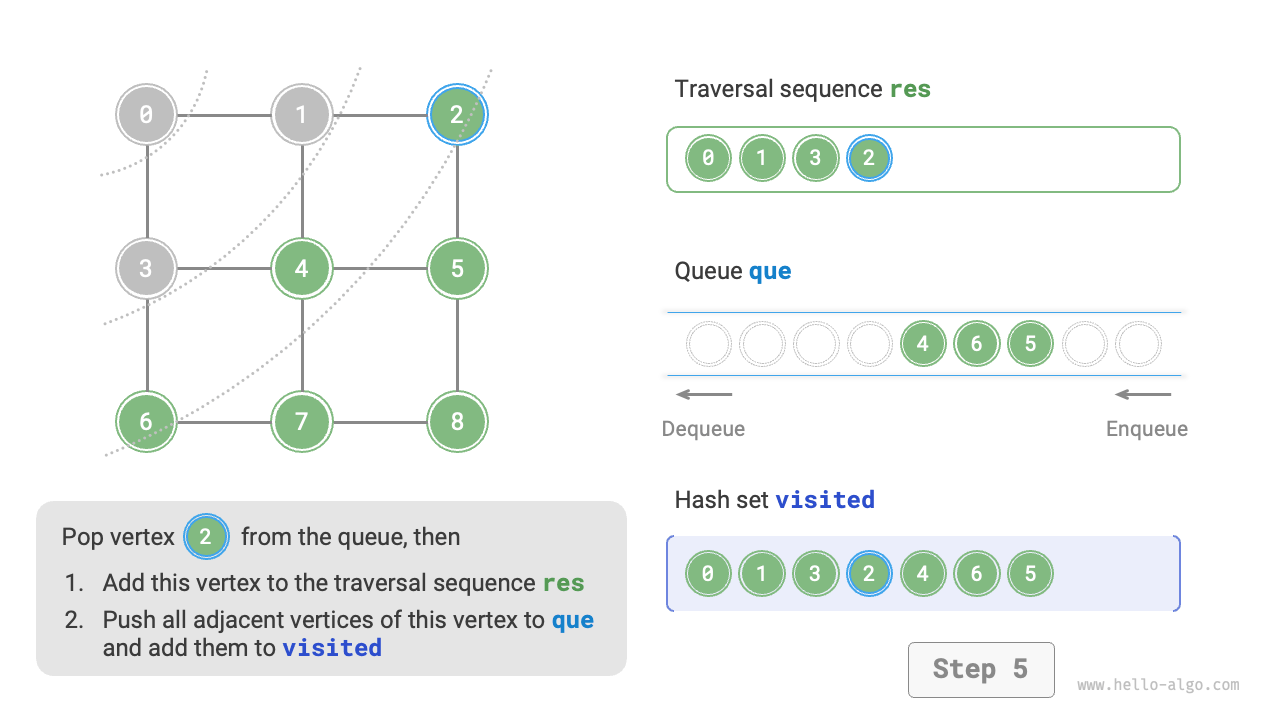
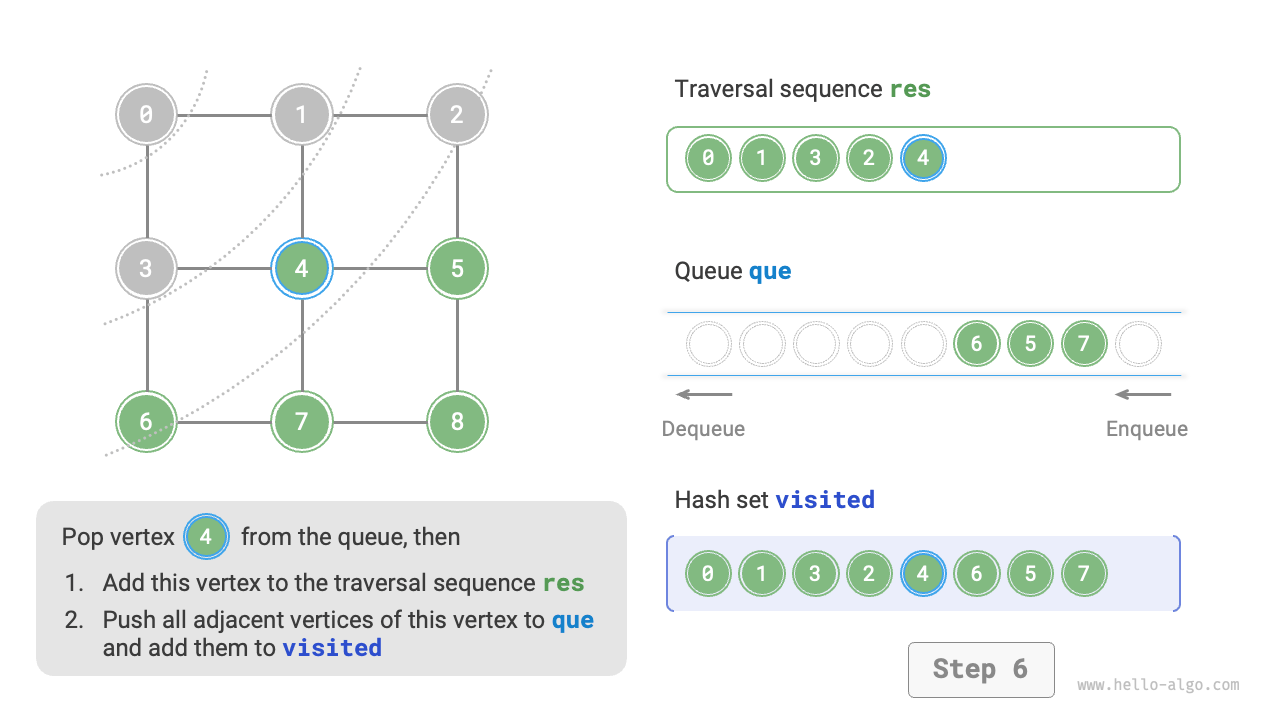
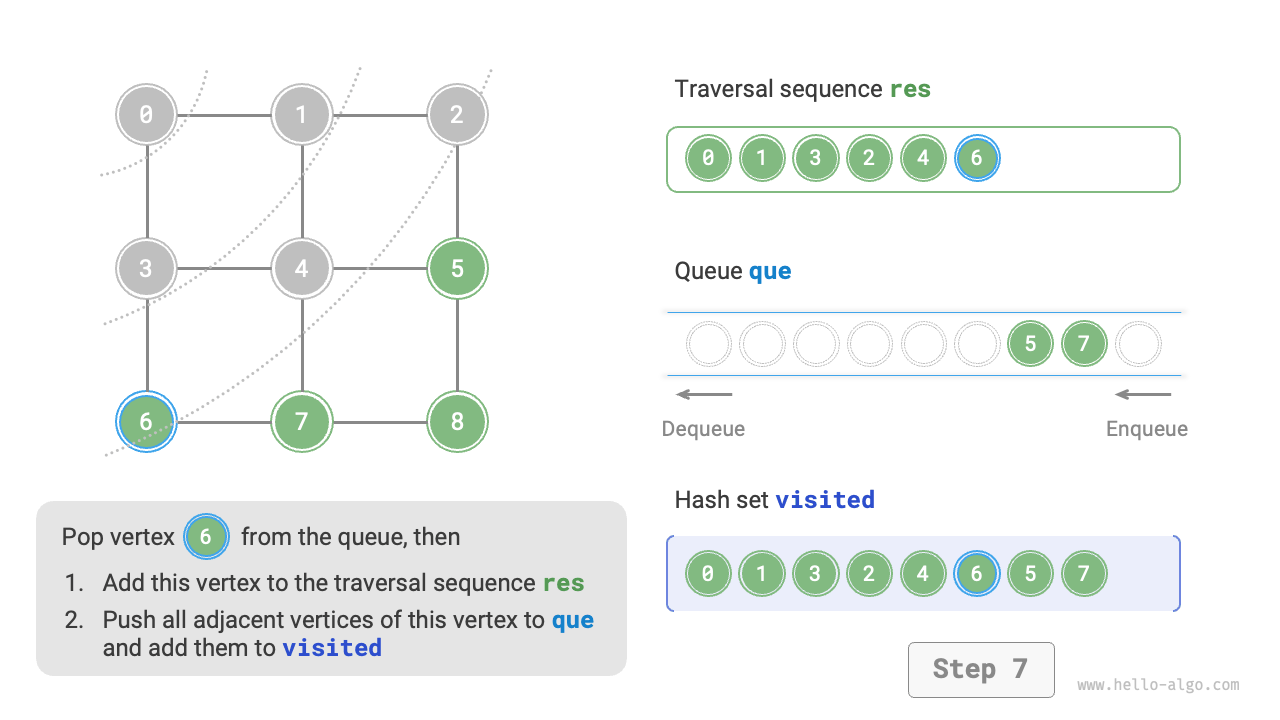
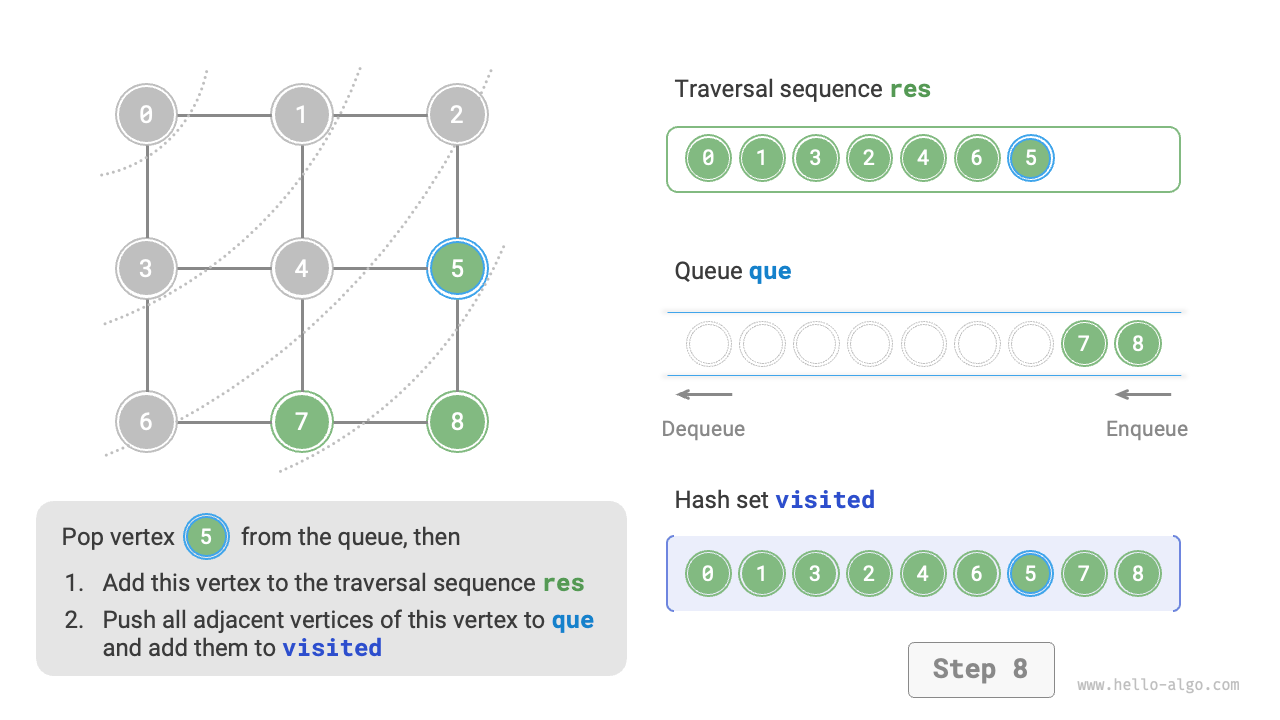
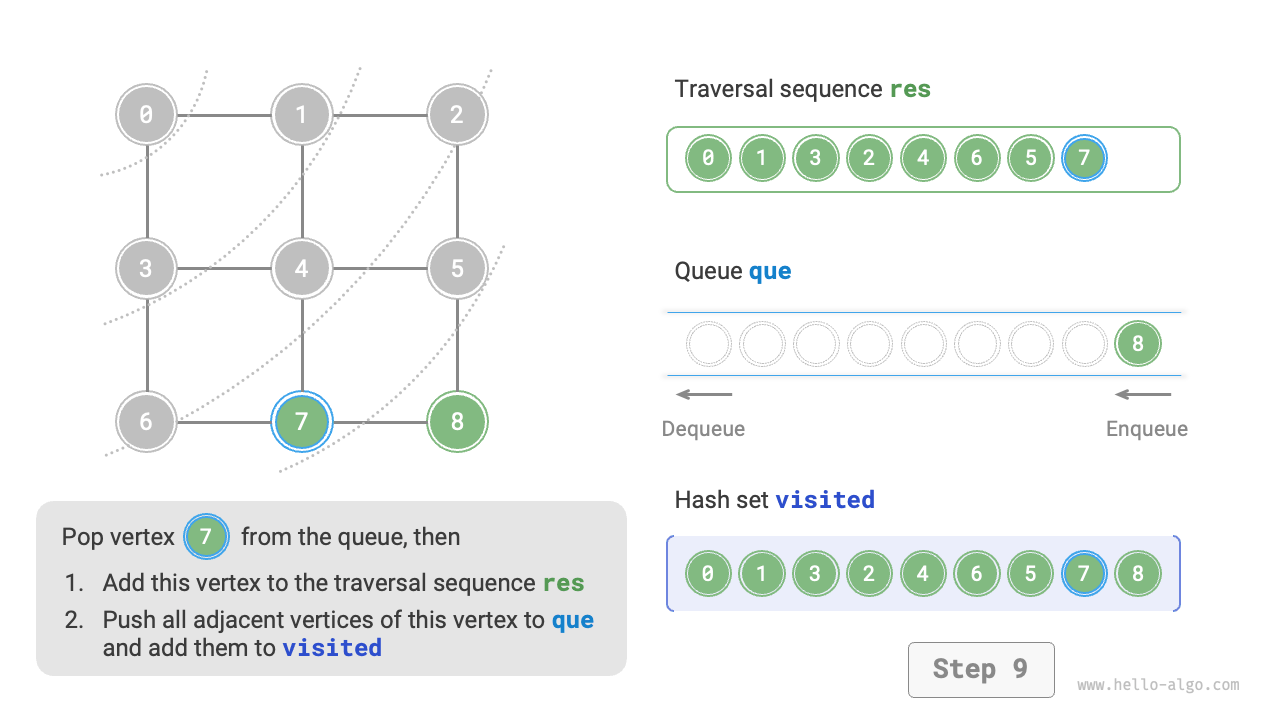
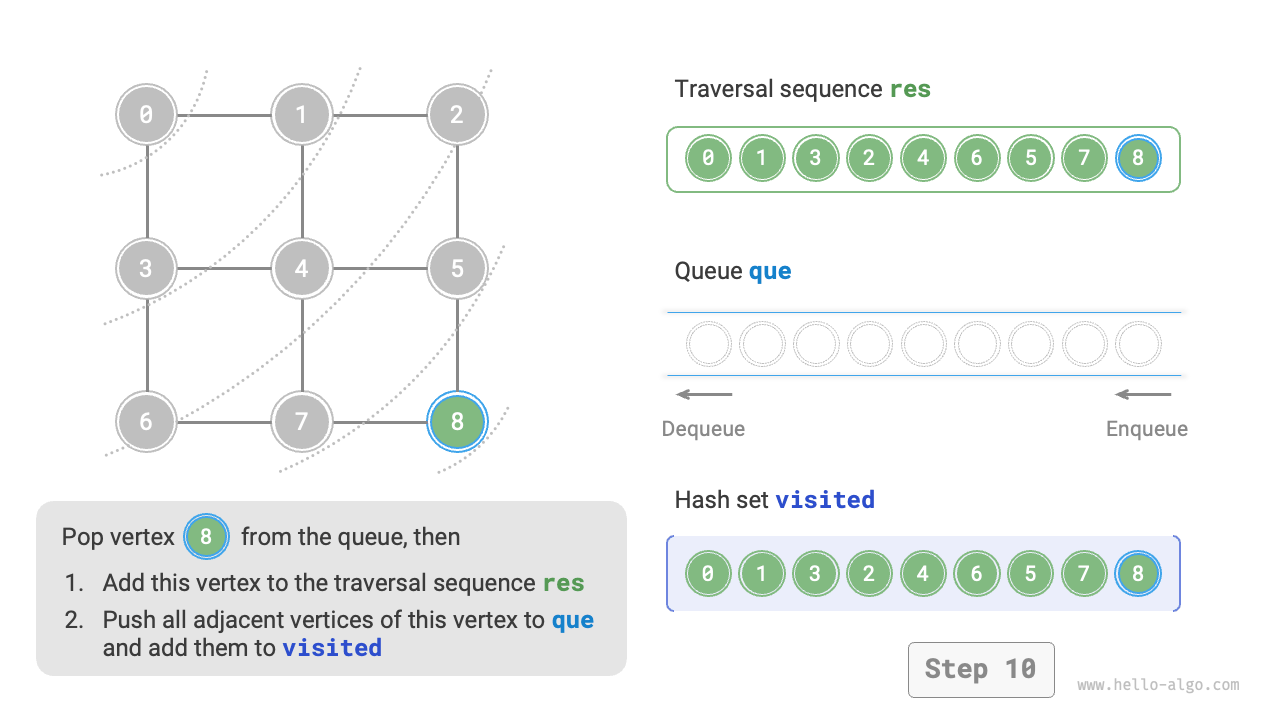
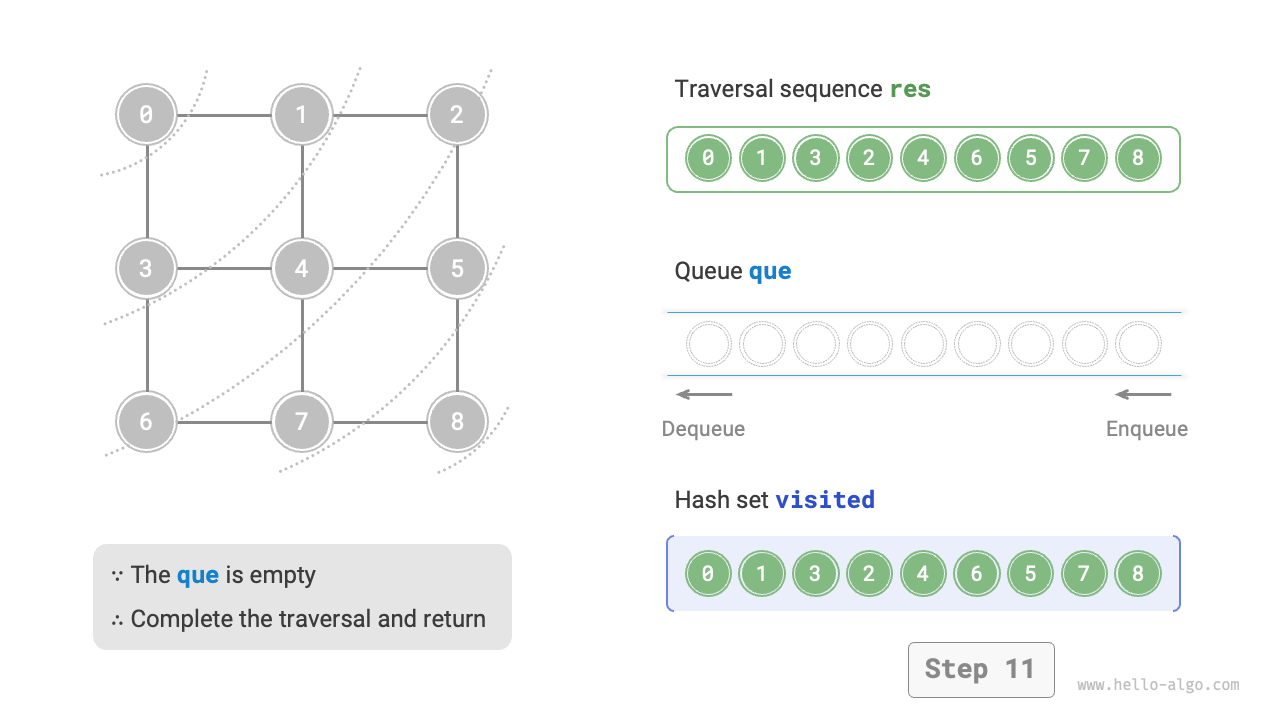
The code is relatively abstract, you can compare it with Figure 9-10 to get a better understanding.
Figure 9-10 Steps of breadth-first search of a graph
Is the sequence of breadth-first traversal unique?
Not unique. Breadth-first traversal only requires traversing in a "near to far" order, and the traversal order of the vertices with the same distance can be arbitrary. For example, in Figure 9-10, the visit order of vertices \(1\) and \(3\) can be swapped, as can the order of vertices \(2\), \(4\), and \(6\).
2. Complexity analysis¶
Time complexity: All vertices will be enqueued and dequeued once, using \(O(|V|)\) time; in the process of traversing adjacent vertices, since it is an undirected graph, all edges will be visited \(2\) times, using \(O(2|E|)\) time; overall using \(O(|V| + |E|)\) time.
Space complexity: The maximum number of vertices in list res, hash set visited, and queue que is \(|V|\), using \(O(|V|)\) space.
9.3.2 Depth-first search¶
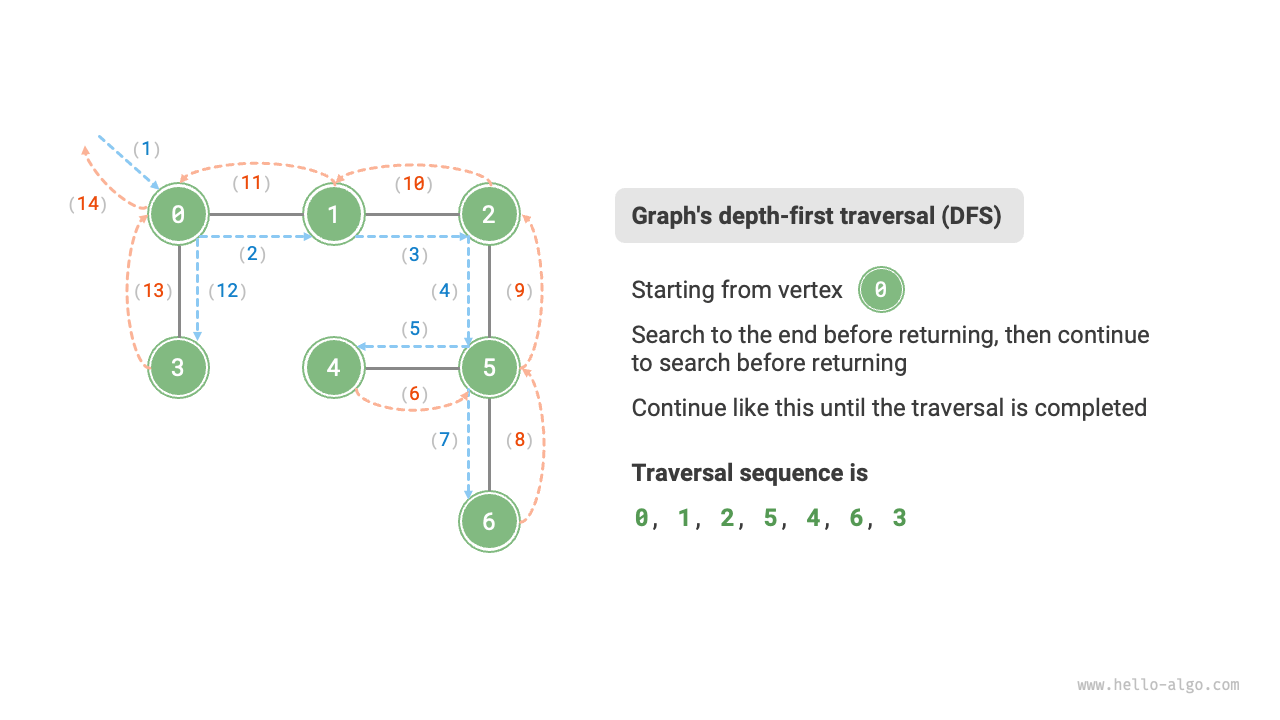
Depth-first search is a traversal method that prioritizes going as far as possible and then backtracks when no further path is available. As shown in Figure 9-11, starting from the top left vertex, visit some adjacent vertex of the current vertex until no further path is available, then return and continue until all vertices are traversed.
Figure 9-11 Depth-first traversal of a graph
1. Algorithm implementation¶
This "go as far as possible and then return" algorithm paradigm is usually implemented based on recursion. Similar to breadth-first search, in depth-first search, we also need the help of a hash set visited to record the visited vertices to avoid revisiting.
def dfs(graph: GraphAdjList, visited: set[Vertex], res: list[Vertex], vet: Vertex):
"""Depth-first traversal helper function"""
res.append(vet) # Record visited vertex
visited.add(vet) # Mark the vertex as visited
# Traverse all adjacent vertices of that vertex
for adjVet in graph.adj_list[vet]:
if adjVet in visited:
continue # Skip already visited vertices
# Recursively visit adjacent vertices
dfs(graph, visited, res, adjVet)
def graph_dfs(graph: GraphAdjList, start_vet: Vertex) -> list[Vertex]:
"""Depth-first traversal"""
# Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
# Vertex traversal sequence
res = []
# Hash set, used to record visited vertices
visited = set[Vertex]()
dfs(graph, visited, res, start_vet)
return res
/* Depth-first traversal helper function */
void dfs(GraphAdjList &graph, unordered_set<Vertex *> &visited, vector<Vertex *> &res, Vertex *vet) {
res.push_back(vet); // Record visited vertex
visited.emplace(vet); // Mark the vertex as visited
// Traverse all adjacent vertices of that vertex
for (Vertex *adjVet : graph.adjList[vet]) {
if (visited.count(adjVet))
continue; // Skip already visited vertices
// Recursively visit adjacent vertices
dfs(graph, visited, res, adjVet);
}
}
/* Depth-first traversal */
// Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
vector<Vertex *> graphDFS(GraphAdjList &graph, Vertex *startVet) {
// Vertex traversal sequence
vector<Vertex *> res;
// Hash set, used to record visited vertices
unordered_set<Vertex *> visited;
dfs(graph, visited, res, startVet);
return res;
}
/* Depth-first traversal helper function */
void dfs(GraphAdjList graph, Set<Vertex> visited, List<Vertex> res, Vertex vet) {
res.add(vet); // Record visited vertex
visited.add(vet); // Mark the vertex as visited
// Traverse all adjacent vertices of that vertex
for (Vertex adjVet : graph.adjList.get(vet)) {
if (visited.contains(adjVet))
continue; // Skip already visited vertices
// Recursively visit adjacent vertices
dfs(graph, visited, res, adjVet);
}
}
/* Depth-first traversal */
// Use adjacency list to represent the graph, to obtain all adjacent vertices of a specified vertex
List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
// Vertex traversal sequence
List<Vertex> res = new ArrayList<>();
// Hash set, used to record visited vertices
Set<Vertex> visited = new HashSet<>();
dfs(graph, visited, res, startVet);
return res;
}
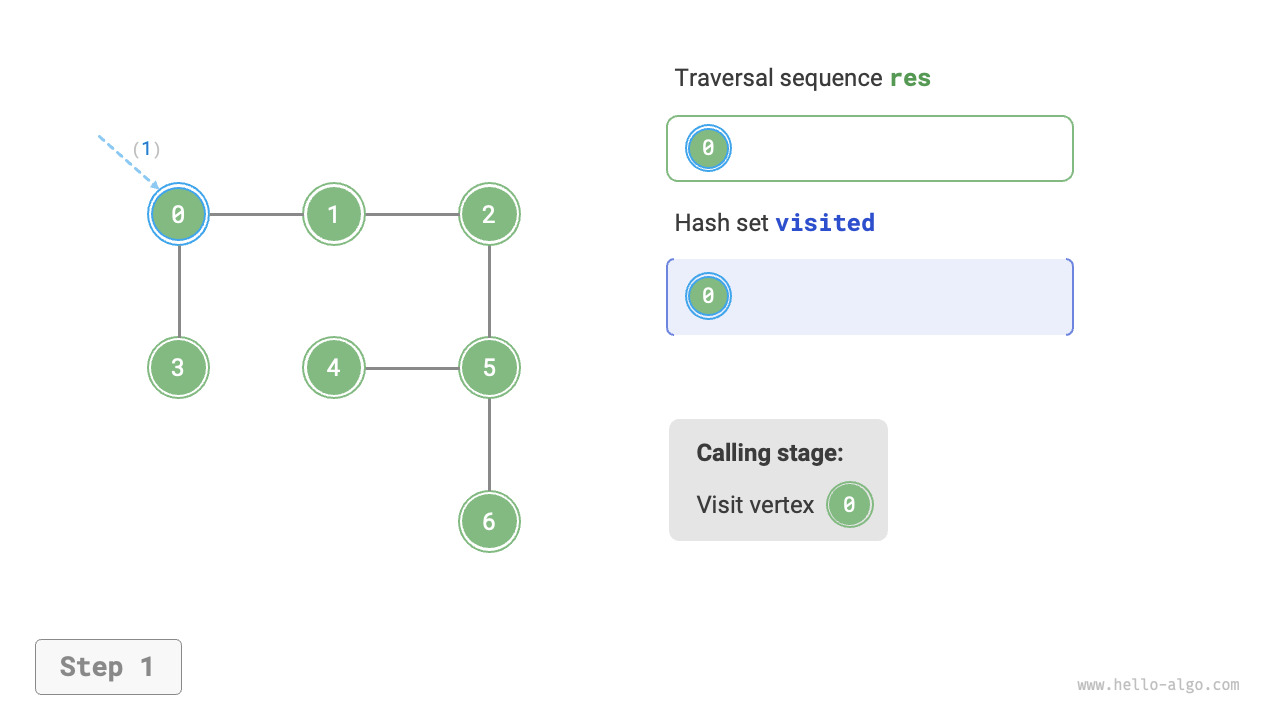
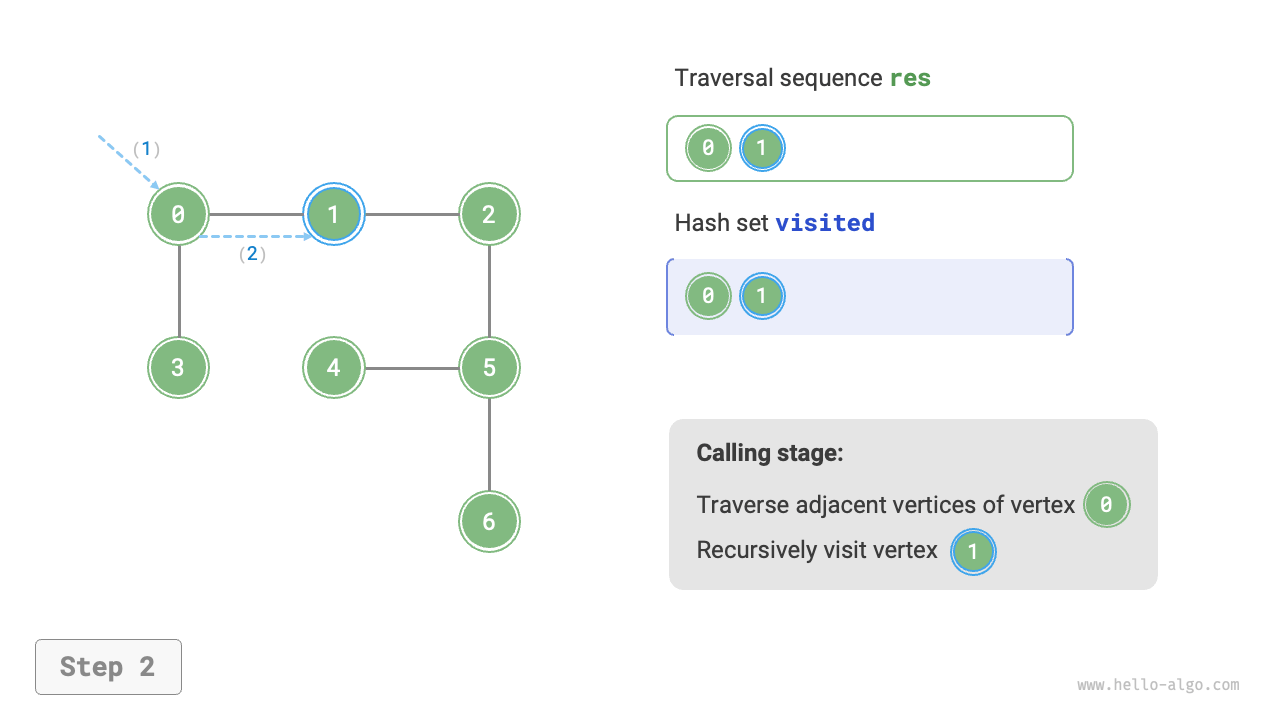
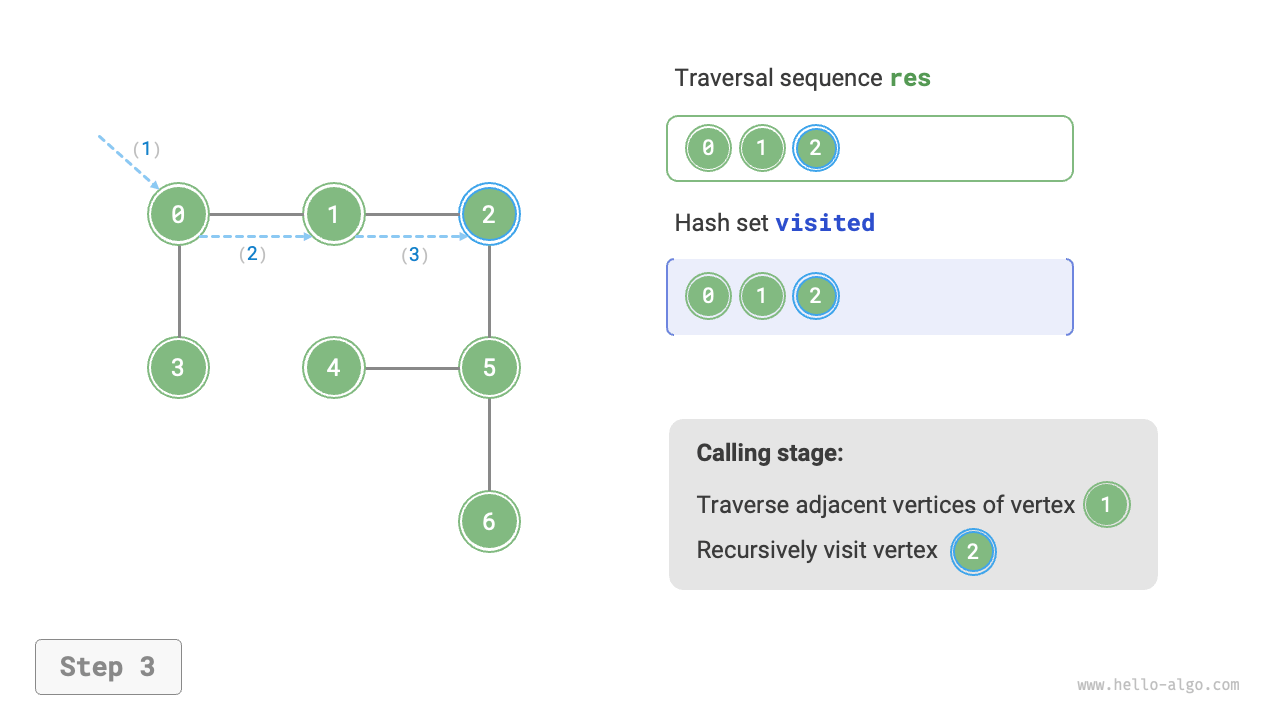
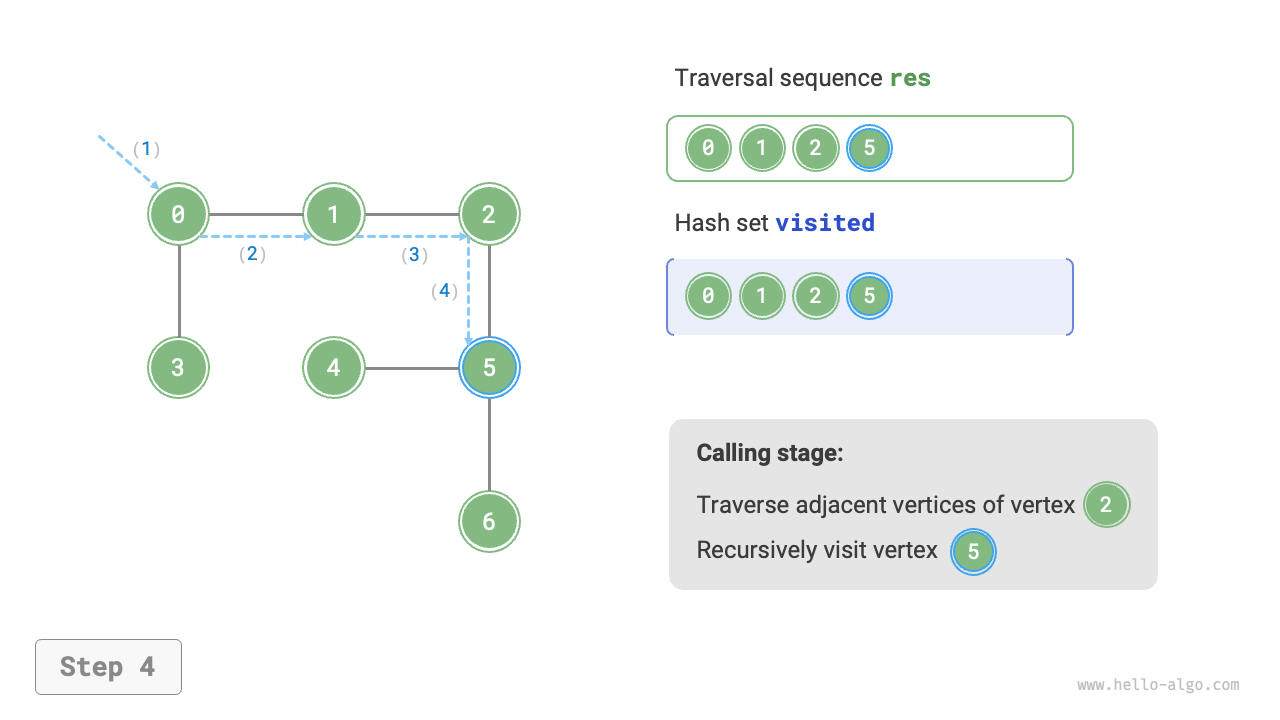
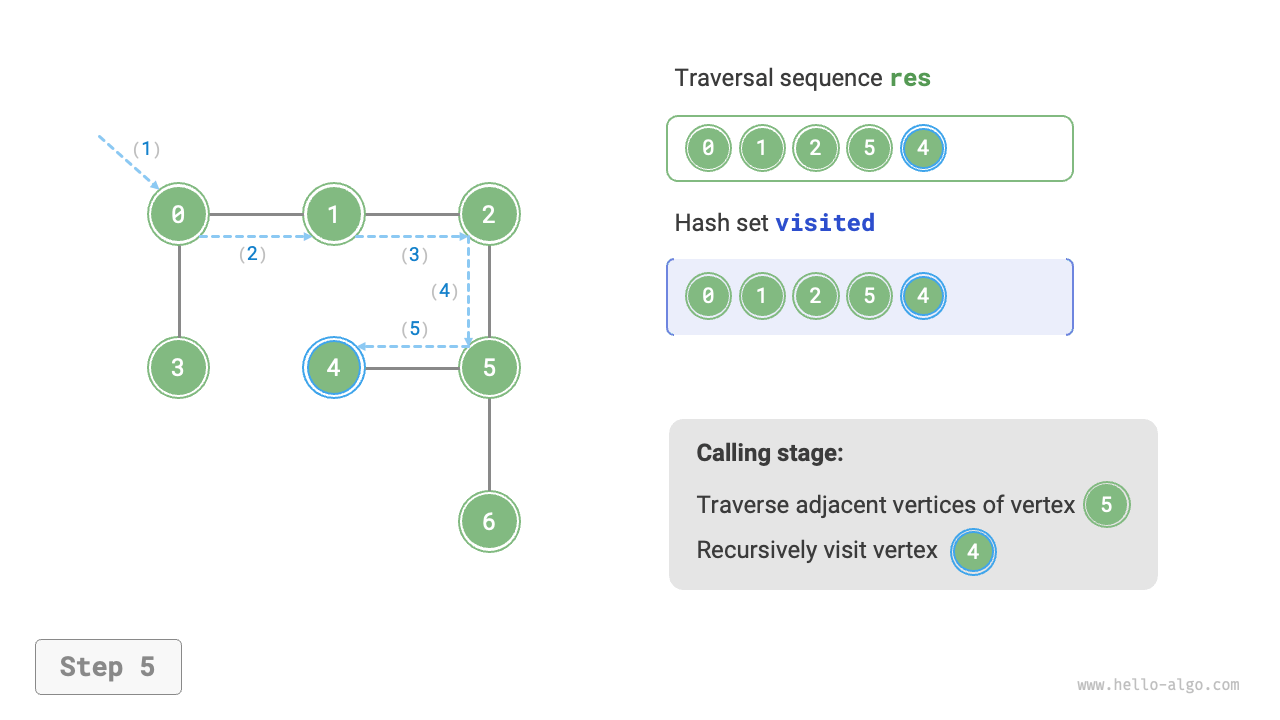
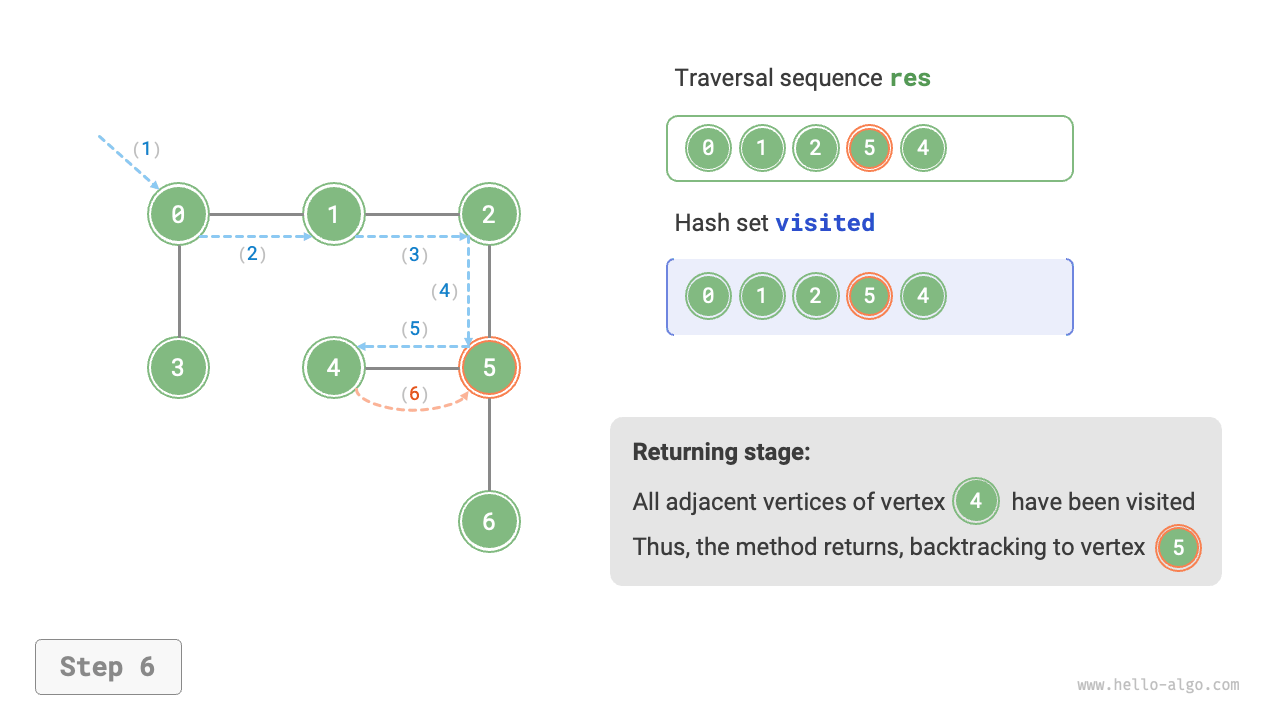
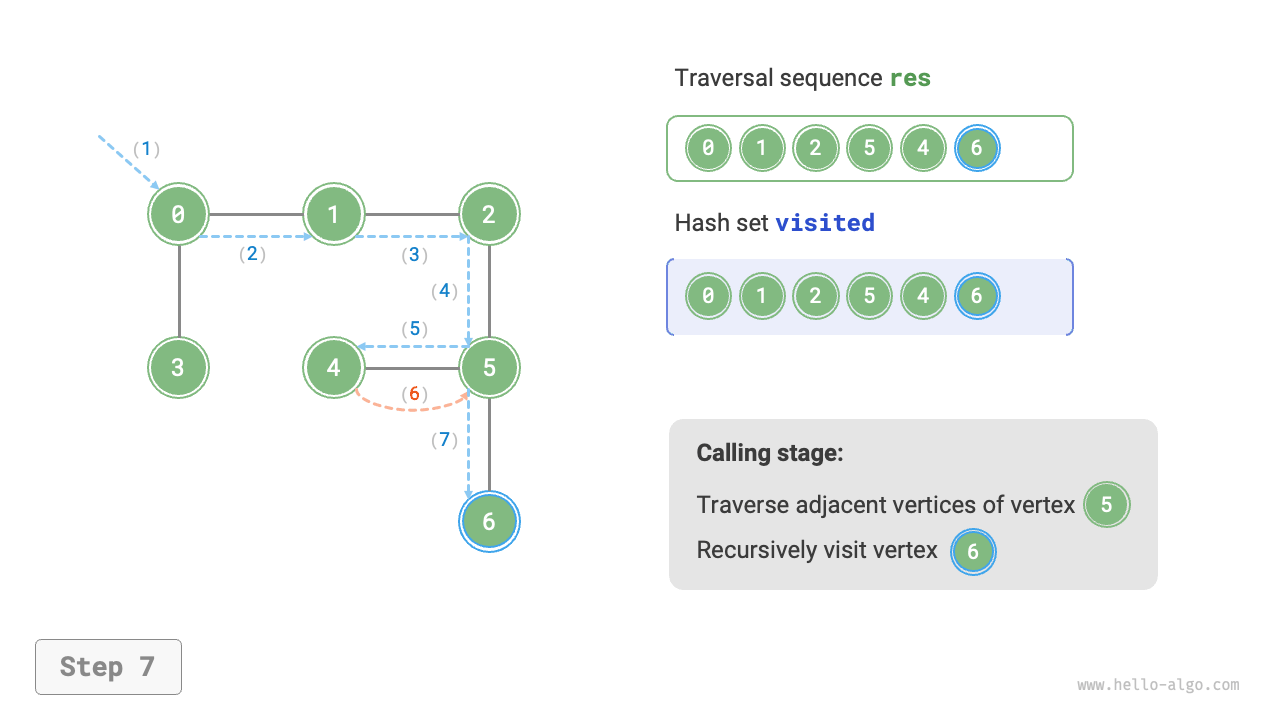
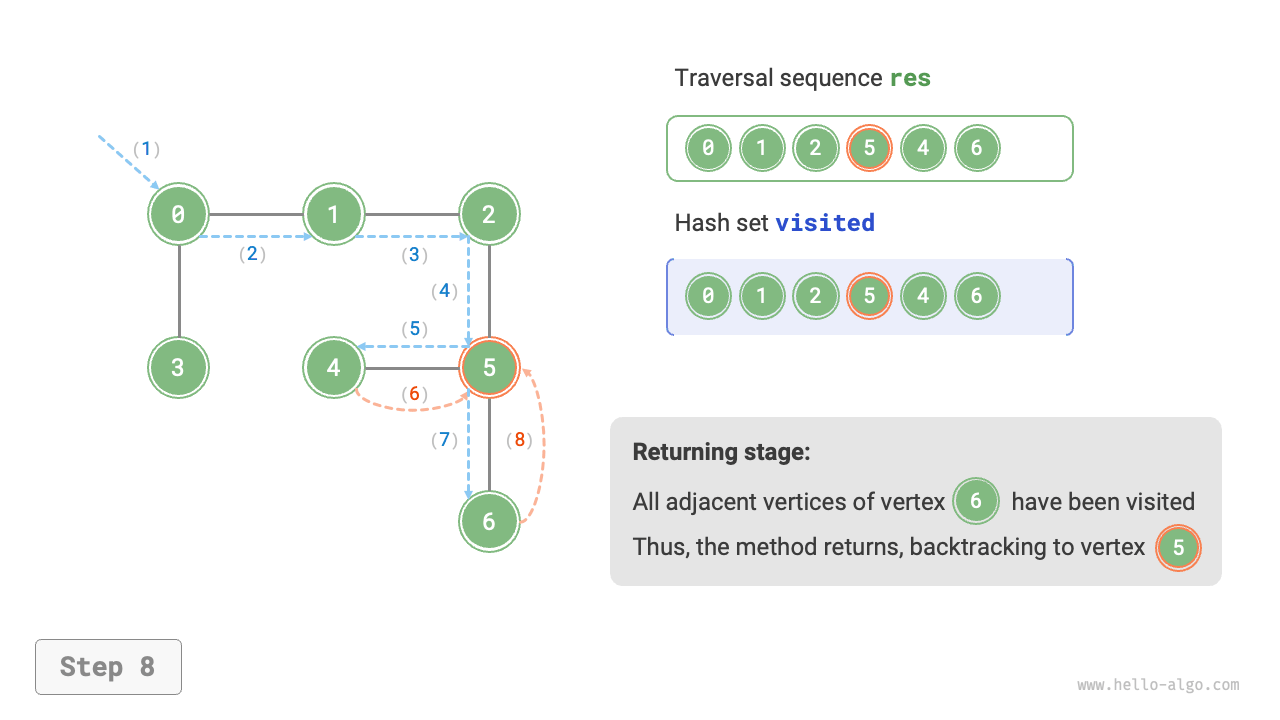
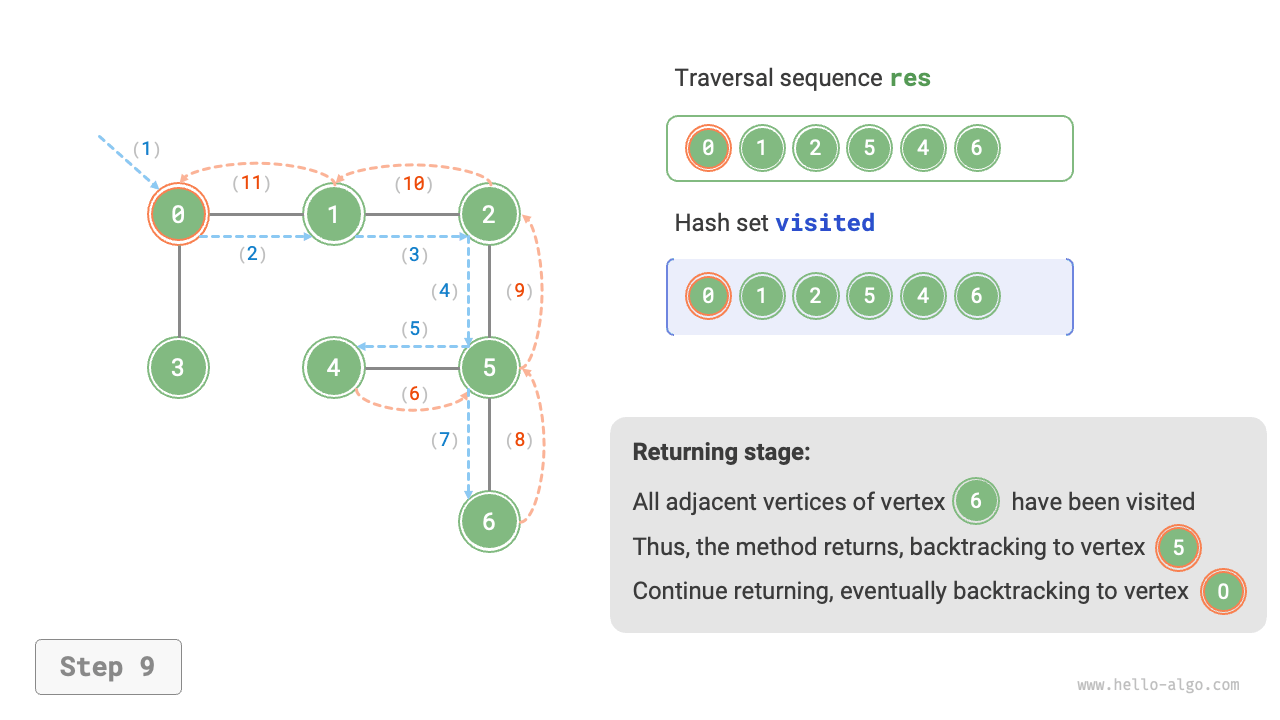
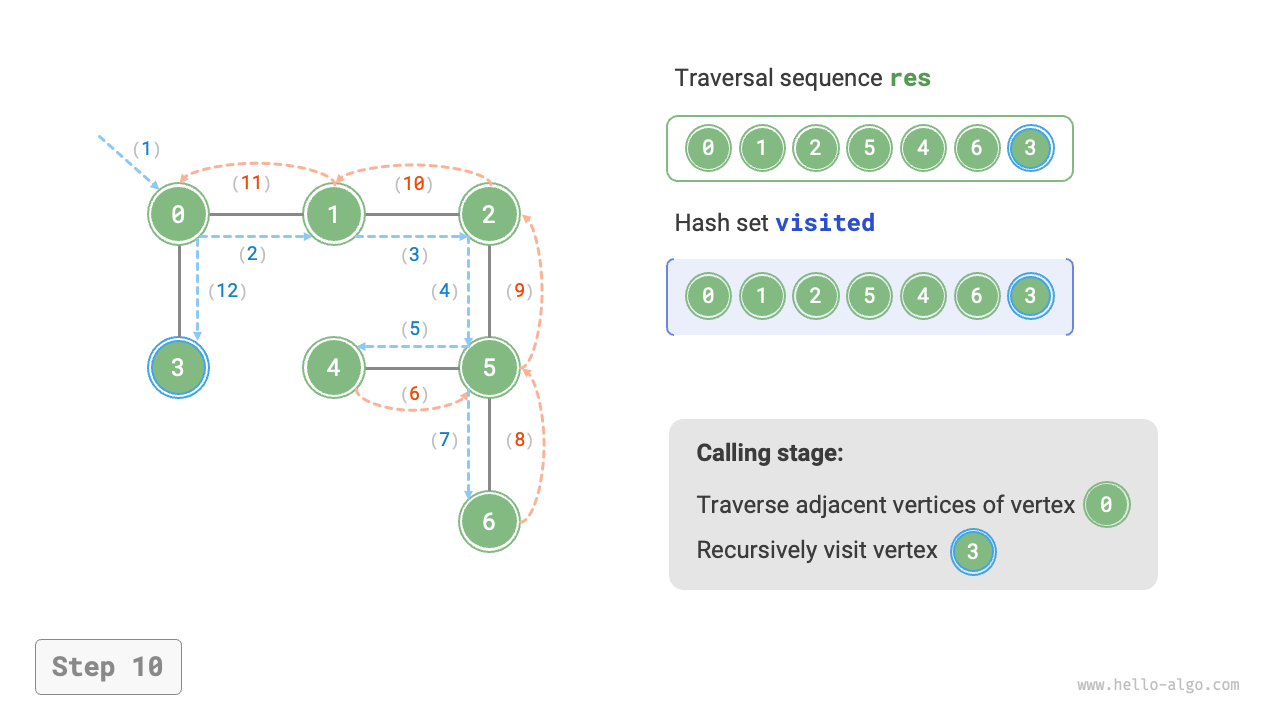
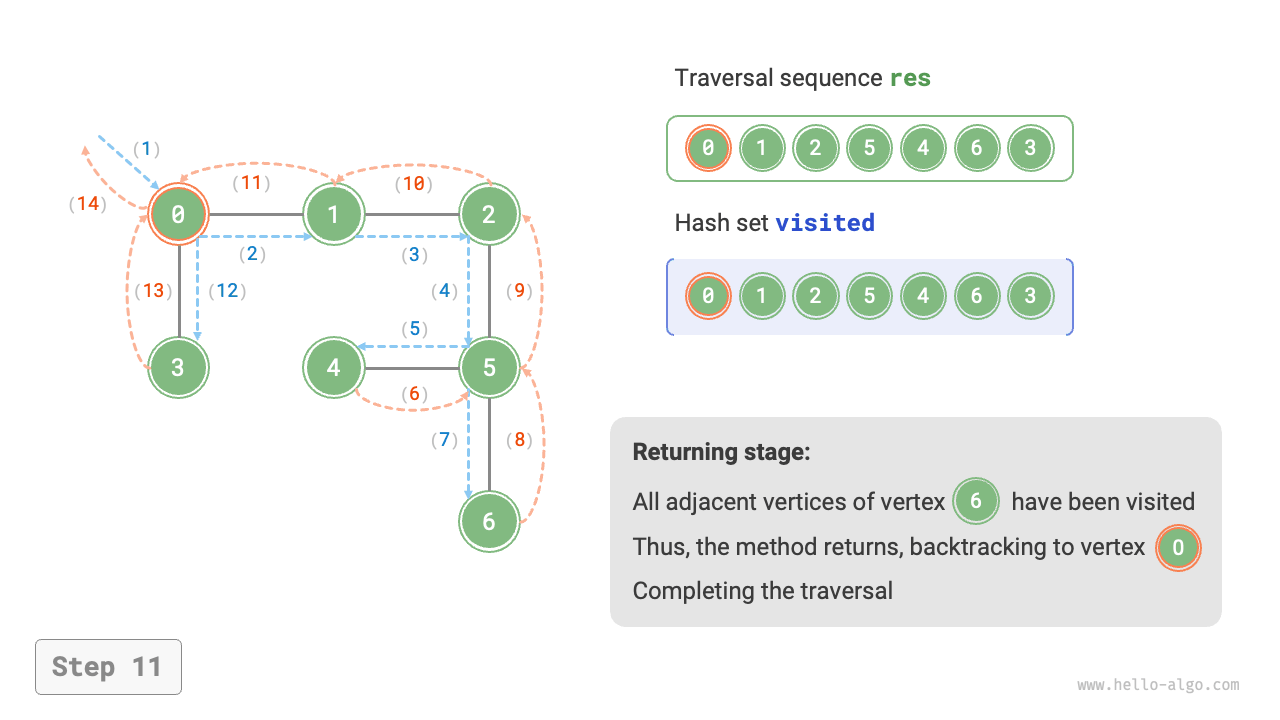
The algorithm process of depth-first search is shown in Figure 9-12.
- Dashed lines represent downward recursion, indicating that a new recursive method has been initiated to visit a new vertex.
- Curved dashed lines represent upward backtracking, indicating that this recursive method has returned to the position where this method was initiated.
To deepen the understanding, it is suggested to combine Figure 9-12 with the code to simulate (or draw) the entire DFS process in your mind, including when each recursive method is initiated and when it returns.
Figure 9-12 Steps of depth-first search of a graph
Is the sequence of depth-first traversal unique?
Similar to breadth-first traversal, the order of the depth-first traversal sequence is also not unique. Given a certain vertex, exploring in any direction first is possible, that is, the order of adjacent vertices can be arbitrarily shuffled, all being part of depth-first traversal.
Taking tree traversal as an example, "root \(\rightarrow\) left \(\rightarrow\) right", "left \(\rightarrow\) root \(\rightarrow\) right", "left \(\rightarrow\) right \(\rightarrow\) root" correspond to pre-order, in-order, and post-order traversals, respectively. They showcase three types of traversal priorities, yet all three are considered depth-first traversal.
2. Complexity analysis¶
Time complexity: All vertices will be visited once, using \(O(|V|)\) time; all edges will be visited twice, using \(O(2|E|)\) time; overall using \(O(|V| + |E|)\) time.
Space complexity: The maximum number of vertices in list res, hash set visited is \(|V|\), and the maximum recursion depth is \(|V|\), therefore using \(O(|V|)\) space.